Question

Consider that a \[{d^6}\] metal ion (\[{M^{2 + }}\]) forms a complex with aqua ligands, and the spin only magnetic moment of the complex is 4.90 BM. The geometry and the crystal field stabilisation energy of the complex is:
A. Tetrahedral and \[-0.6{\Delta _t}\]
B. Tetrahedral and \[-1.6{\Delta _t} + {\rm{ }}1P\]
C. Octahedral and \[-1.6{\Delta _0}\]
D. Octahedral and \[-2.4{\Delta _0} + {\rm{ }}2P\]

Answer 1

Hint: From the given spin-only magnetic moment the number of unpaired electrons can be calculated. The crystal field stabilisation energy can be calculated from the d-orbital splitting pattern in tetrahedral and octahedral situations.

Complete Step by Step Solution:
The spin-only magnetic moment of a transition metal is given by the formula \[\sqrt {n(n + 2)} \] where n = the number of unpaired electrons in the valence shell of the transition metal atom. In the question, the spin-only magnetic moment is given as 4.90 BM. Therefore, we have \[\sqrt {n(n + 2)} = 4.90\]\[ \Rightarrow n = 4\]which means in the d6 metal ion there are four unpaired electrons in its valence d-orbital.

Here, the metal ion forms a complex with aqua ligands (\[{H_2}O\]) which is a comparatively strong field ligand. If the complex formed is octahedral, then the degenerate d-orbitals of the metal ion will split into two sets. Due to the repulsion of the d-orbitals lying along the coordinate axes (\[{d_{{x^2} - {y^2}}},{d_{{z^2}}}\]) with the incoming aqua ligands, energies of the \[{d_{{x^2} - {y^2}}}\]and \[{d_{{z^2}}}\]orbitals will increase comparatively. The \[{d_{{x^2} - {y^2}}}\]and \[{d_{{z^2}}}\]orbitals are called the \[{e_g}\]set while the \[{d_{xy}},{d_{yz}}{\rm{ and }}{{\rm{d}}_{xz}}\]orbitals form the \[{t_{2g}}\]set. This splitting is known as crystal field splittingand the energy separation is denoted as \[{\Delta _o}\]. The \[{e_g}\]orbitals increase in energy by \[ + 0.6{\Delta _o}\]and the \[{t_{2g}}\]orbitals decrease in energy by \[ - 0.4{\Delta _o}\].

Image:d-orbital splitting in octahedral complexes
In this case, the crystal field stabilization energy (CFSE) is calculated as \[CFS{E_o} = 4 \times ( - 0.4{\Delta _o}) + 2 \times ( + 0.6{\Delta _o}) = - 0.4{\Delta _o}\]

If the complex were tetrahedral, energies of \[{d_{xy}},{d_{yz}}{\rm{ and }}{{\rm{d}}_{xz}}\]orbitals (the \[{t_2}\]set) would increase. The splitting is shown below.

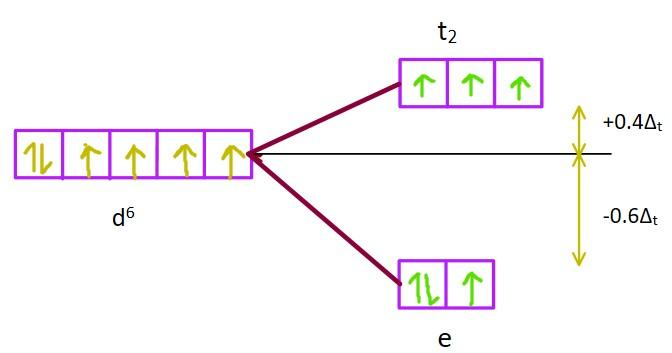
Image: d-orbital splitting in tetrahedral complexes.
In this case, the crystal field stabilization energy (CFSE) is calculated as \[CFS{E_t} = 3 \times ( - 0.6{\Delta _t}) + 3 \times ( + 0.4{\Delta _t}) = - 0.6{\Delta _t}\].
Thus, option A is correct.

Note: The order with respect to \[{\rm{[A]}}\]is \[{\rm{1}}\]and the order with respect to \[{\rm{[B]}}\] is \[{\rm{2}}\]. The overall order for the reaction will be \[(1 + 2)\, = 3\]. This implies that the reaction is of third order overall. Also, the units of rate constant (\[{\rm{k}}\]) for the given reaction can be calculated.
${\rm{rate}}\,\, = \,{\rm{k[A}}{{\rm{]}}^1}{{\rm{[B]}}^2}\\ $
$\Rightarrow {\rm{k}} = \dfrac{{{\rm{rate}}}}{{{{{\rm{[A]}}}^{\rm{1}}}{{{\rm{[B]}}}^{\rm{2}}}}}\\ \Rightarrow {\rm{k}} = \dfrac{{{\rm{mol}}{{\rm{L}}^{{\rm{ - 1}}}}{\rm{mi}}{{\rm{n}}^{{\rm{ - 1}}}}}}{{{{{\rm{(mol}}{{\rm{L}}^{{\rm{ - 1}}}}{\rm{)}}}^{\rm{1}}}{{{\rm{(mol}}{{\rm{L}}^{{\rm{ - 1}}}}{\rm{)}}}^{\rm{2}}}}}\\$
$ \Rightarrow {\rm{k}} = {\rm{mo}}{{\rm{l}}^{ - 2}}{{\rm{L}}^2}{\rm{mi}}{{\rm{n}}^{{\rm{ - 1}}}}$
The units of rate constant is found to be \[{\rm{mo}}{{\rm{l}}^{ - 2}}{{\rm{L}}^2}{\rm{mi}}{{\rm{n}}^{{\rm{ - 1}}}}\].