Question

Consider a frame that is made up of two thin massless rods AB and AC as shown in the figure. A vertical force \[\overrightarrow P \]of magnitude 100 N is applied at point A of the frame. Suppose the force \[\overrightarrow P \] is resolved parallel to the arms AB and AC of the frame. The magnitude of the resolved component along the arm AC is x N. Find the value of x, to the nearest integer? [Given: \[\sin ({35^0}) = 0.573\] , \[\cos ({35^0}) = 0.819\] , \[\sin ({110^0}) = 0.939\], \[\cos ({110^0}) = - 0.342\]]

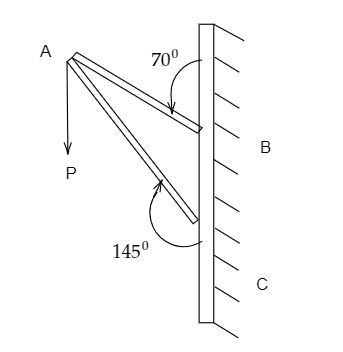
Answer 1

Hint: Before we proceed into the problem, it is important to know about the resolution of vectors.it is defined as the splitting up of a single vector into two or more vectors in different directions which produces a similar effect as it is produced by a single vector. The vectors which are formed after splitting are called component vectors.

Formula Used:
To find the component along AC we have,
\[{P_{AC}} = P\cos \theta \]…….. (1)
Where, \[{P_{AC}}\] is the vertical force component along AC and P is the vertical force acting on a frame.

Complete step by step solution:
Let’s solve this problem now.

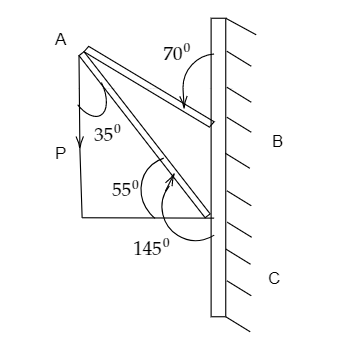
Image: Frame made up of two thin massless rods AB and AC.

In order to find the value of \[\varphi \]we have,
\[\varphi = {180^0} - {110^0} - {35^0}\]
\[\Rightarrow \varphi = {35^0}\]
To find the AC component of P by formula we need the value of\[\theta \]which can be written as,
\[\theta + \varphi = {70^0}\]
\[\Rightarrow \theta = {70^0} - {35^0}\]
\[ \Rightarrow \theta = {35^0}\]
From the equation (1) we are going to find the value of \[{P_{AC}}\]
\[{P_{AC}} = P\cos \theta \]
\[\Rightarrow {P_{AC}} = 100 \times \cos {35^0}\].............(By data we have,\[\cos ({35^0}) = 0.819\])
\[\Rightarrow {P_{AC}} = 100 \times 0.819\]
\[\Rightarrow {P_{AC}} = 81.9N\]
\[\Rightarrow {P_{AC}} = 82N = xN\]
\[ \therefore x = 82\]

Therefore, the value of x is 82.

Note: If any vector quantity is said to be resolved, then it will resolve into two components, one is vertical and other one is horizontal. The vertical component tells us about the upward influence of the force which is applicable in this diagram. The magnitude of a vector basically defines the length of the vector.