Question

Charges are placed on the vertices of a square as shown. Let $\vec{E}$ be the electric field lines and $V$ be the potential at the centre. If the charges on A and B are interchanged with those on D and C respectively, then:
A) $\vec{E}$ changes, $V$ remains unchanged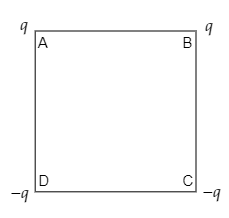
B) $\vec{E}$ remains unchanged, $V$ remains changes
C) Both $\vec{E}$ and $V$ change
D) $\vec{E}$ and $V$ remain unchanged

Answer 1

Hint: The magnitude of the potential at the centre of the square will be the potential due to all the charges. The electric field is a vector quantity and hence will have a direction as well as a magnitude. The magnitude of the electric field vector at the centre of the square will remain the same after the interchanging of the charges but the direction of the resultant field is due to the electric fields between A and C and that between B and D and hence may change.

Formula used:
The potential at a point is given by, $\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{r}$ where ${{\varepsilon }_{0}}$ is the permittivity of free space, $q$ is the charge and $r$ is the distance between the point and the charge.

Complete step by step answer:
Step 1: Sketch the given system of charges before and after the interchanging of charges.
Let $r$ be the distance from the centre to each charge placed on the vertices of the square.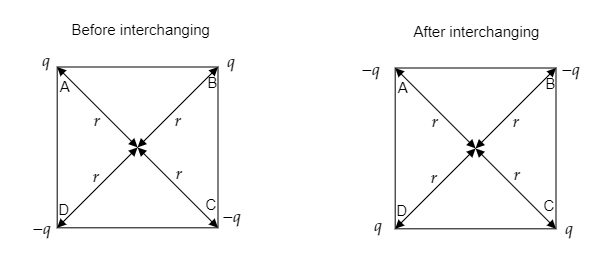
Step 2: Express the potential at the centre before and after the interchanging of charges.
The potential at the centre of the square is the sum of the potential at the centre due to each charge.
So before interchanging the potential can be expressed as $V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{q}{r} \right)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{q}{r} \right)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{-q}{r} \right)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{-q}{r} \right)=0$
Now after the interchanging of charges at A and B with those at D and C respectively, the potential at the centre will be $V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{-q}{r} \right)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{-q}{r} \right)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{q}{r} \right)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{q}{r} \right)=0$
So the potential remains the same before and after the interchanging.
Step 3: Sketch the electric field lines before and after the interchanging of charges.
To determine the direction of the resultant electric field at the centre of the square, we consider diagonally opposite charges i.e, the charges at A and C and those at B and D.
Now before interchanging, ${{\vec{E}}_{AC}}$ will be the field due to charges $q$ at A and $-q$ at C and ${{\vec{E}}_{BD}}$ will be the field due to charges $q$ at B and $-q$ at D.
However, after interchanging the direction of the fields will change. So ${{\vec{E}}_{CA}}$ will be the field due to charges $-q$ at A and $q$ at C and ${{\vec{E}}_{DB}}$ will be the field due to charges $-q$ at B and $q$ at D. This is sketched in the figure below.
So the potential remains unchanged but the electric field line changes direction.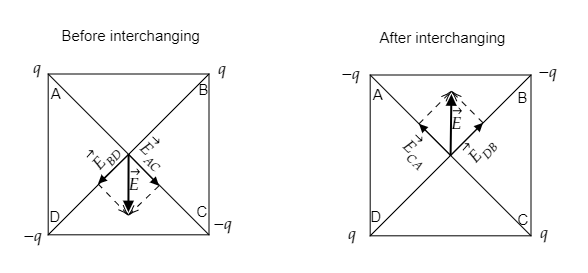

Hence the correct option is A.

Note: For a square, the diagonals are equal in length and are perpendicular bisectors. So we take the distance from the centre of the square to each charge placed at the corners of the square to be the same. The direction of the electric field lines will be from the positive charge to the negative charge. The resultant electric field direction is obtained using the parallelogram law of vectors.