Question

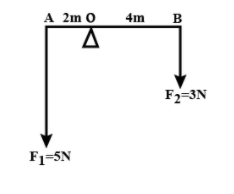
Calculate total moment of the two forces about O from the given figure:



A. $2{\text{ Nm (clockwise)}}$
B. $2{\text{ Nm (anti clockwise)}}$
C. ${\text{4 Nm (clockwise)}}$
D. ${\text{4 Nm (anti clockwise)}}$

Answer 1

Hint Moment of force is a measure of tendency of the force to cause rotation in a body about a specific point or axis. Its value is equal to that of torque and is given by $\tau = \vec r \times \vec F$ where $\vec F$ is the force in consideration and $\vec r$ is the position vector of force with respect to a fixed point about which moment is to be calculated.
The direction of the moment of force is given by the right hand thumb rule which states that if we roll our fingers from $\vec r$ towards the force $\vec F$ then the direction of thumb gives the direction of the moment of force.

Complete step by step answer
Let us first discuss the moment of a force.
Moment of force is a measure of tendency of the force to cause rotation in a body about a specific point or axis. Its value is equal to that of torque and is given by $\tau = \vec r \times \vec F$ where $\vec F$ is the force in consideration and $\vec r$ is the position vector of force with respect to a fixed point about which moment is to be calculated.
The direction of the moment of force can be found out by the basic rule of cross product or by the right hand thumb rule which states that if we roll our fingers from $\vec r$ towards the force $\vec F$ then the direction of thumb gives the direction of the moment of force.
Now, let us consider the force ${F_1}$ .
The position vector from point O has magnitude $r = 2m$ which is at right angle to the force.
Since, $\tau = \vec r \times \vec F = r \times F \times \sin 90^\circ = r \times F$
Therefore, for force ${F_1}$ , moment about O is given by
${\tau _1} = 2 \times 5 = 10{\text{ Nm (anti clockwise)}}$
Now, for force ${F_2}$ , the position vector about O has magnitude $r = 4m$ which is also perpendicular to the force. So, the moment about O is given by
${\tau _2} = 4 \times 3 = 12{\text{ Nm (clockwise)}}$
Let us consider the clockwise direction to be positive. Therefore, the net moment of the forces about the point O will be the vector sum of the two forces and given by
$\tau = 12 - 10 = 2{\text{ Nm (clockwise)}}$

Hence, option A is correct.

Note Although the unit of torque and moment is the same that is ‘Nm’ but there are certain differences between them. Torque is related to the movement but the moment is a static force. Torque can be used to measure the coupling whereas moment is not used for this purpose.