Question

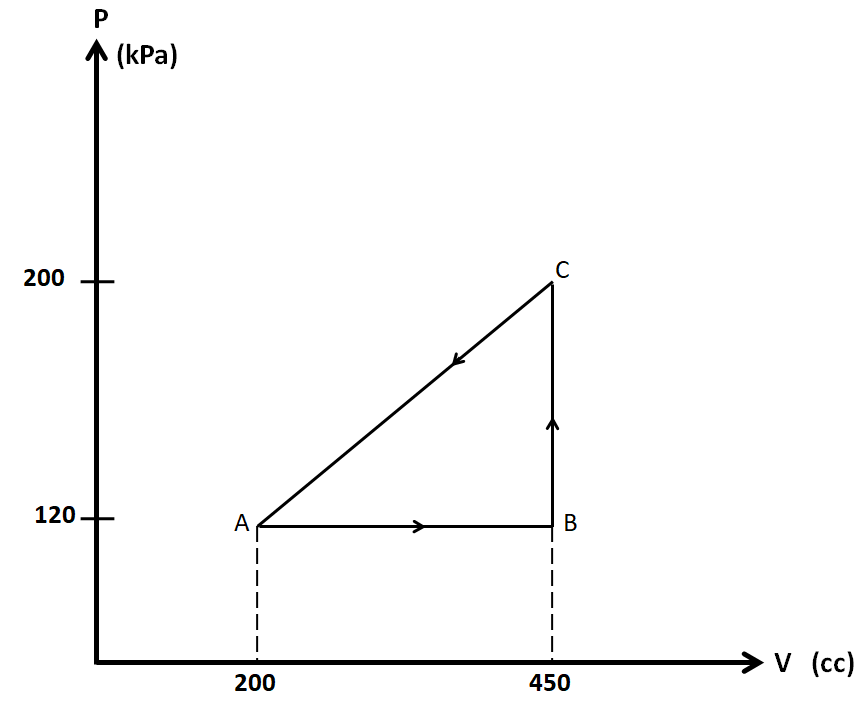
Calculate the work done by the gas in the diagram.

(A) $30J$
(B) $20J$
(C) $ - 20J$
(D)$ - 10J$

Answer 1

Hint: To solve this question, we need to find out the area under the curve of each of the three processes given in the diagram. Then from the sign convention, we can find out the work done in each of these processes. These individual works have to be added to get the final answer.

Complete step-by-step answer:
In the diagram given in the question, we have a thermodynamic cycle which consists of three states, A, B, and C.
We have the pressures at these states as ${P_A} = {P_B} = 120kPa$, ${P_C} = 200kPa$
We know that $1kPa = 1000Pa$. So we have
${P_A} = {P_B} = 1.2 \times {10^5}Pa$ …………………….(1)
${P_C} = 2 \times {10^5}Pa$ ………………………..(2)
Also, the volumes are ${V_A} = 200cc$, ${V_B} = {V_C} = 450cc$
We know that $1cc = {10^{ - 6}}{m^3}$
So we have
${V_A} = 2 \times {10^{ - 4}}{m^3}$ ………………………….(3)
${V_B} = {V_C} = 4.5 \times {10^{ - 4}}{m^3}$ …………...……….(4)
Now, we know that the work done is equal to the area under the PV curve.
So we consider each of the three processes AB, BC, and AC separately.
Process AB:
As the pressure is constant in this process, so this is the isobaric process.
We know that the work done in an isobaric process is
$W = P\Delta V$
So the work done in this process is given by
${W_1} = {P_A}\left( {{V_B} - {V_A}} \right)$
Substituting (1), (3) and (4)
\[{W_1} = 1.2 \times {10^5}\left( {4.5 \times {{10}^{ - 4}} - 2 \times {{10}^{ - 4}}} \right)\]
\[ \Rightarrow {W_1} = 1.2 \times {10^5} \times 2.5 \times {10^{ - 4}}\]
On solving we get
\[{W_1} = 30J\] …………………….(5)
Process BC:
As the volume is constant in this process, so the process BC is isochoric.
We know that the work done in an isochoric process is equal to zero.
So the work done in this process is
\[{W_2} = 0\] ………………….(6)
Process CA:
The PV diagram is a straight line in this process, so we cannot name it. So we have to use the general expression for the work done.
We consider the PV diagram of this process separately.

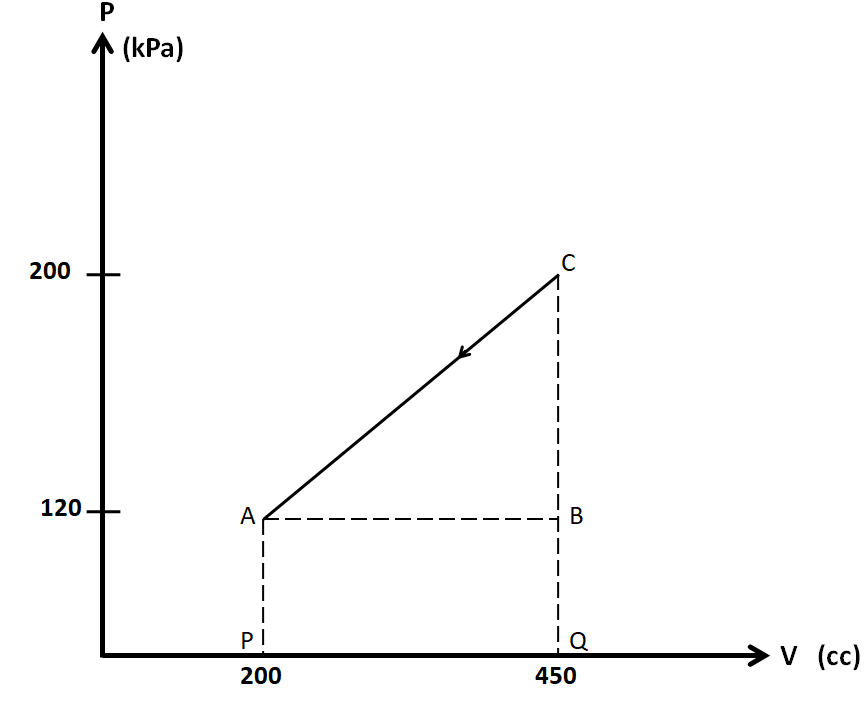
We know that the work done is equal to the area under the PV curve. As we can see in the above figure, the area under the line CA consists of the triangle ABC, and the rectangle ABQP. So the total area under this curve is given by
$A = \dfrac{1}{2} \times AB \times BC + AB \times BQ$
\[A = \dfrac{1}{2} \times \left( {{V_B} - {V_A}} \right) \times \left( {{P_C} - {P_B}} \right) + \left( {{V_B} - {V_A}} \right) \times \left( {{P_B} - 0} \right)\]
From (1), (2), (3) and (4) we get
\[A = \dfrac{1}{2} \times \left( {4.5 \times {{10}^{ - 4}} - 2 \times {{10}^{ - 4}}} \right) \times \left( {2 \times {{10}^5} - 1.2 \times {{10}^5}} \right) + \left( {4.5 \times {{10}^{ - 4}} - 2 \times {{10}^{ - 4}}} \right) \times 1.2 \times {10^5}\]
\[ \Rightarrow A = \dfrac{1}{2} \times \left( {2.5 \times {{10}^{ - 4}}} \right) \times \left( {0.8 \times {{10}^5}} \right) + \left( {2.5 \times {{10}^{ - 4}}} \right) \times 1.2 \times {10^5}\]
On solving we get
$A = 2.5 \times {10^{ - 4}} \times 1.6 \times {10^5}$
\[ \Rightarrow A = 40J\]
Now, the volume in this process is decreasing. So the work done should be negative. Therefore we have the work done in this process as
${W_3} = - 40J$ ………………………..(7)
Now, the total work in this cycle is
$W = {W_1} + {W_2} + {W_3}$
From (5), (6), and (7) we get
$W = 30 + 0 - 40$
$ \Rightarrow W = - 10J$
Thus, the work done by the gas in the given diagram is equal to $ - 10J$.

Hence, the correct answer is option D.

Note: We should not ignore the directions of the arrows. They decide the sign of the work done. Also, we could attempt this question by calculating the area of the triangle present in the given diagram. Then considering the anticlockwise direction of the arrows, the work done will be equal to the negative of this area.