Question

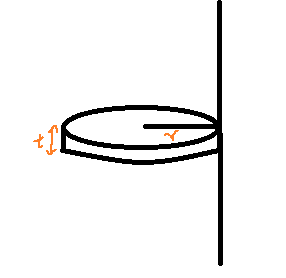
Calculate the radius of gyration of the disc of radius r and thickness t about a line perpendicular to the plane of this disk and tangent to the disk as shown in the figure.

Answer 1

: Hint: The radius of gyration is defined mathematically as the root mean square distance of the object parts from the center of mass or a given axis. We can calculate the radius of gyration if we know the moment of inertia and the total mass of the body.

Complete step by step answer:
So in the question we are given a circular disc of radius r and thickness t. Suppose this disc has a density $\text{ }\!\!\rho\!\!\text{ }$ associated with it and the volume of the disc is given by, $\text{V}=\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{2}}}\text{t}$.
So the total mass of the disk can be written as, $\text{M}=\text{ }\!\!\rho\!\!\text{ V}$, which is equal to,
$\text{M}=\text{ }\!\!\rho\!\!\text{ }\left( \text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{2}}}\text{t} \right)$ …equation (1)
So the moment of inertia of any body can be written as,
\[\text{I}=\text{M}{{\text{K}}^{\text{2}}}\]
Where,
I is the moment of inertia
M is the total mass of the body
K is the radius of gyration
So the radius of gyration of any extended body can be written as,
$\text{K}=\sqrt{\dfrac{\text{I}}{\text{M}}}$ ….. equation (2)
Suppose we have an axis that passes perpendicular to the center of the disc.
The moment of inertia of a circular disc of radius R is given by,
$\text{I}=\dfrac{\text{M}{{\text{R}}^{\text{2}}}}{2}$ … equation (3)
Substituting the values of I and M from equation (1) and (3) respectively in equation (2), we get
$\text{K}=\sqrt{\dfrac{(\text{M}{{\text{r}}^{\text{2}}})/2}{\text{ }\!\!\rho\!\!\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{2}}}\text{t}}}=\sqrt{\dfrac{\text{M}{{\text{r}}^{\text{2}}}}{\text{2M}}}$
$\therefore \text{K}=\dfrac{\text{r}}{\sqrt{2}}$
So the radius of gyration along an axis which is perpendicular to the disc is given by $\text{K}=\dfrac{\text{r}}{\sqrt{2}}$.
Suppose we have an axis that passes as a tangent to the disc as shown in the figure.
Using the parallel axis theorem, the moment of inertia of a circular disc of radius R along a tangent to the disc is given by,
$\text{I}=\dfrac{\text{M}{{\text{R}}^{\text{2}}}}{2}+\text{M(R}{{\text{)}}^{\text{2}}}$ … equation (4)
Substituting the values of M and I from equation (1) and (4) respectively in equation (2), we get
$\text{K}=\sqrt{\dfrac{(3\text{M}{{\text{r}}^{\text{2}}})/2}{\text{ }\!\!\rho\!\!\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{2}}}\text{t}}}=\sqrt{\dfrac{\text{3M}{{\text{r}}^{\text{2}}}}{\text{2M}}}$
$\therefore \text{K}=\text{r}\sqrt{\dfrac{\text{3}}{\text{2}}}$
So the radius of gyration along an axis which is tangent to the disc is given by $\text{K}=\text{r}\sqrt{\dfrac{\text{3}}{\text{2}}}$.

Note: The radius of gyration is also called gyradius. It can also be defined as the radial distance to a point that would have a moment of inertia the same as the body's actual distribution of mass if the total mass of the body were concentrated.
The moment of inertia is an analog to mass in rotational dynamics.