Question

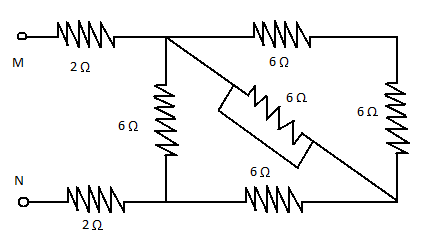
Calculate the equivalent resistance between point M and N.

A) $5\Omega $
B) $6\Omega $
C) $3\Omega $
D) $7\Omega $

Answer 1

Hint: To solve this connection you should know the series connection and parallel connection of resistances. In series connection, the equivalent resistance is simply the sum of the individual resistances connected in series.
In parallel connection, the reciprocal of equivalent resistance is equal to the sum of the reciprocal of individual resistances connected parallelly.

Complete step by step solution:
From the figure resistance ${R_1}$ and ${R_2}$ in series so the equivalent of them will be the direct of sum of their individual resistances,
$R' = {R_1} + {R_2}$
Put the values of ${R_1}$ and ${R_2}$ in the above equation to get the value of resistance.
$R' = 6 + 6$
$\Rightarrow 12\,\Omega$
Similarly, resistance ${R_4}$ and ${R_5}$ are also in series so the equivalent of them will also be the direct of sum of their individual resistances,
$R'' = {R_4} + {R_5}$
Put the values of ${R_4}$ and ${R_5}$ in above equation,
$R'' = 6 + 6$
$ \Rightarrow 12\,\Omega $
Now, we can see that resistance $R',{R_3}$ and $R’’$ are connected by parallel connection so the equivalent resistance of these resistances can be determined as,
$\dfrac{1}{{R'''}} = \dfrac{1}{{R'}} + \dfrac{1}{{{R_3}}} + \dfrac{1}{{R''}}$
Substitute the values of resistances in above equation,
$\dfrac{1}{{R'''}} = \dfrac{1}{{12}} + \dfrac{1}{6} + \dfrac{1}{{12}}\\
\Rightarrow \dfrac{{1 + 2 + 1}}{{12}}\\
\Rightarrow \dfrac{1}{{R'''}} = \dfrac{4}{{12}} = \dfrac{1}{3}\\
\Rightarrow R''' = 3\,\Omega
$
Resistances ${R_6},R'''$ and ${R_7}$ are connected in series so the equivalent resistance of them determined as,
${R_{eq}} = {R_6} + R''' + {R_7}$
Put the values in the above equation to get equivalent resistance.
$ {R_{eq}} = 2 + 3 + 2\\
\Rightarrow 7\,\Omega
$
Thus the equivalent resistance of the circuit is $7\,\Omega $.

Note: In this type of questions equivalent resistance cannot calculate directly. You have to use proper steps to determine equivalent resistance.
Solve the question by breaking it into small circuits and then find step by step resistance. Make sure that resistance connected parallel should be solved by the parallel connection method of equivalent resistance and resistance connected in series connection should be determined by equivalent resistance of series connection method.