Question

At the moment $t = 0$ a particle leaves the origin and moves in the positive direction of the $x - axis$. Its velocity varies with time as $\upsilon = {\upsilon _0}\left( {1 - t/r} \right)$, where ${\upsilon _0}$ is the initial velocity vector whose modulus equals${\upsilon _0} = 10.0cm/s.t = 5.0s$. Find:
$\left( a \right)$ the $x$ coordinate of the particle at the moments of time $6.0,10,{\text{ and 20s}}{\text{.}}$
$\left( b \right)$ the moments when the particles are at the distance $10.0cm$ from the origin,
$\left( c \right)$ the distance $s$ covered by the particle during the first $4.0{\text{ and 8}}{\text{.0s}}$, draw the approximate plot$s\left( t \right)$.

Answer 1

Hint The meaning of speed of an object is outlined because of the rate of change of the object’s position with relation to a frame of reference and time. It would sound difficult however velocity is largely speeding in a very specific direction. It’s a vector quantity, which implies we'd like each magnitude (speed) and direction to outline velocity.

Complete step by step solution:
$\left( a \right)$As the particles leaving the origin at $t = 0$
So,
$ \Rightarrow \vartriangle x = x - \int {{v_x}dt} $
Further expanding it,
$ \Rightarrow \vec v = {\vec v_0}\left( {1 - \dfrac{t}{\tau }} \right)$
Where
$ \Rightarrow {v_x} = {v_0}\left( {1 - \dfrac{t}{\tau }} \right)$
From the above two-equation,
$ \Rightarrow x = \int {{v_0}} \left( {1 - \dfrac{t}{\tau }} \right)dt = {v_0}t\left( {1 - \dfrac{t}{{2\pi }}} \right)$
Hence X coordinate of the particle at $t = 6s$
$ \Rightarrow x = 10 \times 6\left( {1 - \dfrac{6}{{2 \times 5}}} \right)$
On solving the above, we get
$ \Rightarrow 24cm = 0.24m$
Similarly at $t = 10s$
$ \Rightarrow x = 10 \times 10\left( {1 - \dfrac{{10}}{{2 \times 5}}} \right)$
$ \Rightarrow 0m$
Now at $t = 20s$
$ \Rightarrow x = 10 \times 20\left( {1 - \dfrac{{20}}{{2 \times 5}}} \right)$
Further on solving,
$ \Rightarrow - 200cm = - 2m$
$\left( b \right)$. At the moment the particle is at a distance of $10cm$ from the origin,
$ \Rightarrow x = \pm 10cm$
Putting $ \Rightarrow x = \pm 10cm$in the above equation
$ \Rightarrow 10 = 10t\left( {1 - \dfrac{t}{{10}}} \right)$
On simplifying
$ \Rightarrow {t^2} - 10t + 10 = 0$
Now we will find the value of $t$ from here.
$ \Rightarrow t = \dfrac{{10 \pm \sqrt {100 - 40} }}{2}$
On simplifying,
$ \Rightarrow 5 \pm \sqrt {15} s$
Now putting $x = - 10$
We get,
$ \Rightarrow - 10 = 10\left( {1 - \dfrac{t}{{10}}} \right)$
On solving,
$ \Rightarrow t = 5 \pm \sqrt {35s} $
As t cannot be negative, so
$ \Rightarrow t = 5 + \sqrt {35s} $
So the particle is at the following time at three intervals:
$t = 5 + \sqrt {35s} $,$5 \pm \sqrt {15} s$.
$\left( c \right)$. We have
$ \Rightarrow \vec v = {\vec v_0}\left( {1 - \dfrac{t}{\tau }} \right)$
So, $v = \left| {\vec v} \right| = {v_0}\left( {1 - \dfrac{t}{\tau }} \right){\text{ for t}} \leqslant \tau $
And
$ \Rightarrow v = \left| {\vec v} \right| = {v_0}\left( {\dfrac{t}{\tau } - 1} \right){\text{ for t > }}\tau $
Therefore,
$ \Rightarrow s = \int_0^t {{v_0}} \left( {1 - \dfrac{t}{\tau }} \right)dt$ For ${\text{t}} \leqslant \tau = {v_0}t\left( {1 - \dfrac{t}{{2\pi }}} \right)$
And
$ \Rightarrow {v_0}\tau \left[ {1 + {{\left( {1 - \dfrac{t}{\tau }} \right)}^2}} \right]/2$ for $t > \tau \left( A \right)$
Now we will solve the integration,
$ \Rightarrow s = \int_0^4 {{v_0}} \left( {1 - \dfrac{t}{\tau }} \right)dt$
Putting the required value, we get
$ \Rightarrow s = \int_0^4 {10} \left( {1 - \dfrac{t}{5}} \right)dt$
$ \Rightarrow 24cm$
And for $t = 8s$
$ \Rightarrow s = \int_0^5 {10} \left( {1 - \dfrac{t}{5}} \right)dt + \int_5^8 {10} \left( {\dfrac{t}{5} - 1} \right)dt$
On integrating and simplifying, we get
$ \Rightarrow s = 34cm$
Based on the above equations. Graph plot can be drawn as shown below



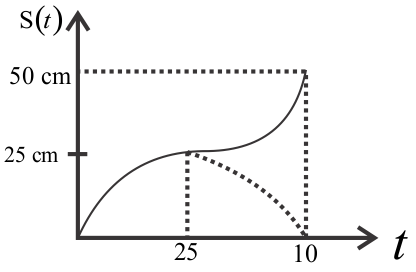
Note: Speed and velocity is a touch confusing for many people. Well, the distinction between speed and velocity is that speed offers us a plan of how briskly an object is moving whereas velocity not solely tells us its speed however additionally tells us the direction the body is taking possession. We can outline speed as a function of distance traveled whereas velocity could be a performance of displacement.