
Assertion:
The \[p{K_a}\]value of (I) is lower than the \[p{K_a}\]of (II).
Reason:Non-aromatic compounds are more stable than anti-aromatic compounds.
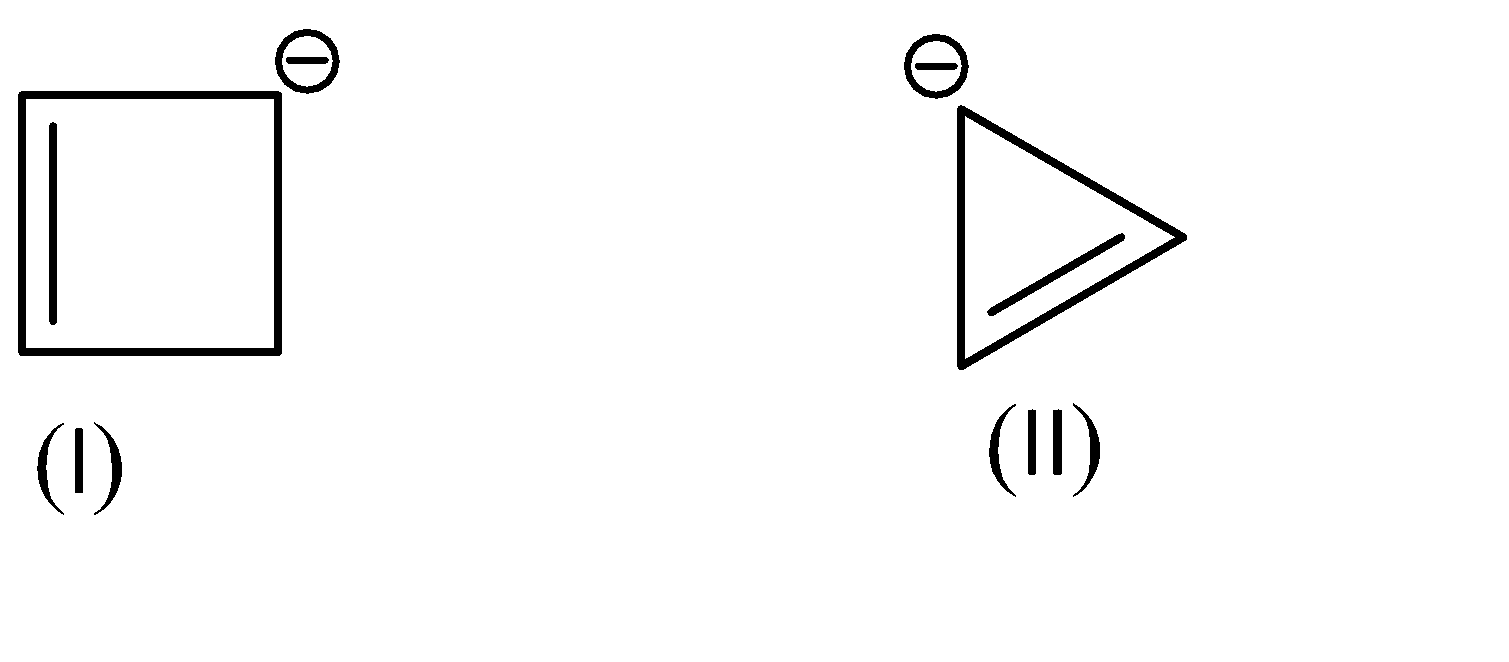
A.Both assertion and reason are correct and the reason is the correct explanation for assertion
B.Both assertion and reason are correct and the reason is not correct explanation for assertion
C.Assertion is correct but reason is incorrect.
D.Assertion is incorrect but the reason is correct.
Answer
233.1k+ views
Hint: Aromatic and Anti-aromatic compounds can be differentiated on the basis of Huckel's Rule.
Complete step by step answer:
We can identify the and classify compounds as either aromatic or anti-aromatic based on the following rules:
1.For a compound to be Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n+2) \[\pi \]electrons, where ‘n’ denotes the number of subsequent energy levels and can be equal to any whole number, i.e. 0,1,2,3,…
2.And for the compound to be Anti-Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n) \[\pi \]electrons
3.If a compound does not have a continuous ring of conjugated p orbitals in a planar conformation, then it is nonaromatic
One important question you must be having is how we identify \[\pi \]electrons. For that, remember the following points. \[\pi \]electrons lie in p orbitals and \[s{p^2}\]hybridized orbitals, each have 1 p orbital. In a completely conjugated molecule, each carbon atom is \[s{p^2}\]hybridized, and hence the electrons present in these p orbitals are \[\pi \]electrons.
As for the compounds given to us,
Compound (I) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.But it does not exhibit resonance
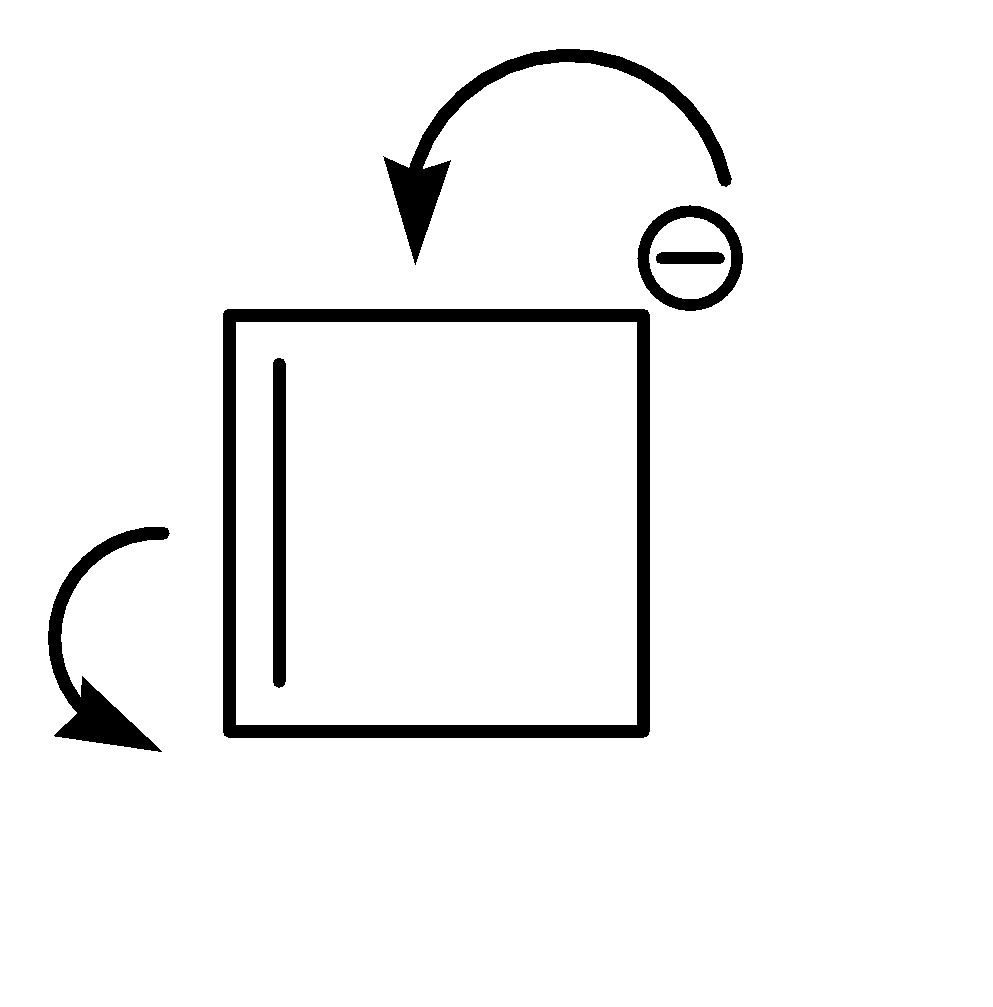
Shifting of electrons would bring us back to the same structure.
On the other hand, Compound (II) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.It does exhibit resonance
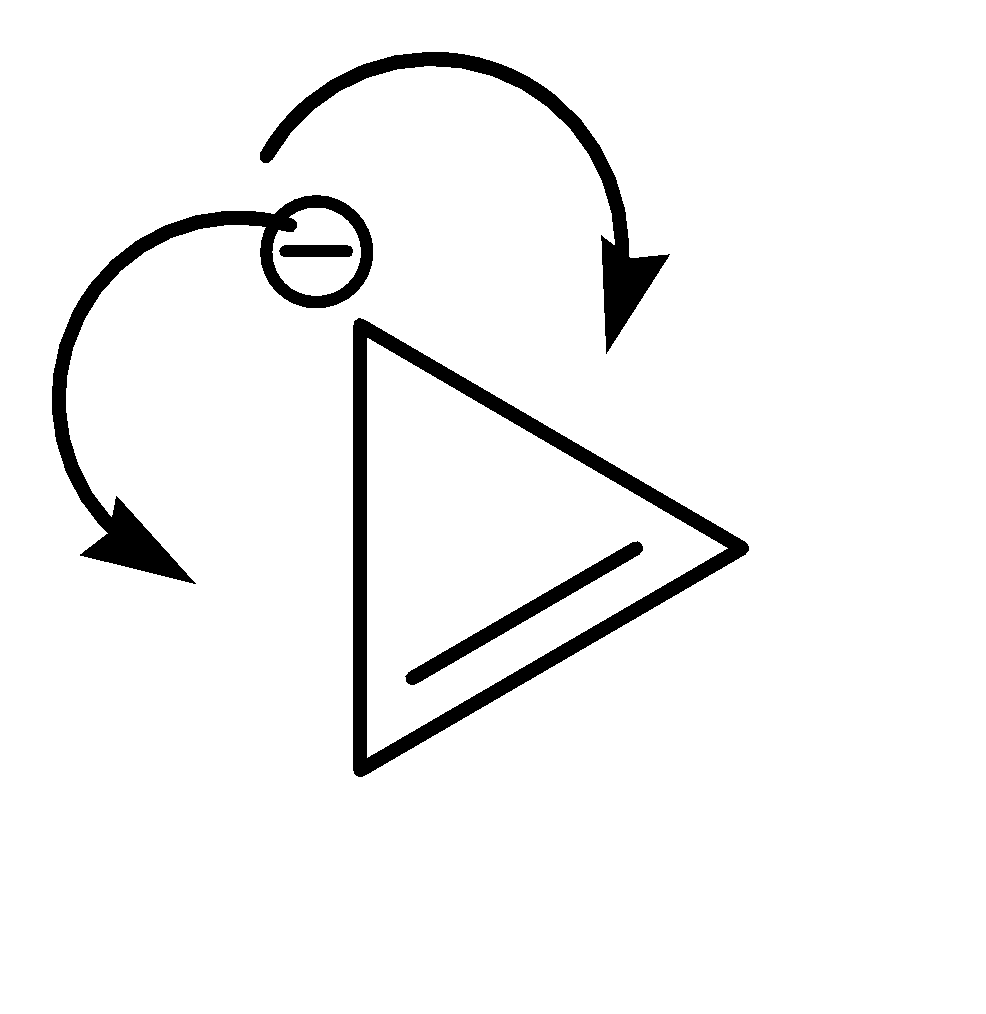
This compound exhibits resonance in both directions.
And it has 4\[\pi \]electrons, which satisfies Huckle’s rule with the value of n=1.
Hence, we can conclude that Compound (I) is Non-Aromatic and Compound (II) is Anti-Aromatic.
-We know that, the trend in the stability of Aromatic, Non-Aromatic and Anti Aromatic compounds is:
Aromatic > Non-Aromatic > Anti-Aromatic
Hence, Anti aromatic compounds are less stable than Non-aromatic Compounds. This means that the conjugate bases of Anti aromatic compounds are more stable than Non-aromatic Compounds. And we know that the increasing stability of the conjugate base increases the acidity of the compound.
Hence Anti aromatic compounds are less acidic than Non-aromatic Compounds.
\[p{K_a}\] is a method used to indicate the strength of an acid. The lower the value of \[p{K_a}\], higher is the strength of the acid.
Now, relating the above conclusions to the given compounds, we get,
\[p{K_a}\] of Compound(I) < \[p{K_a}\]of Compound (II)
Hence, both the reason and assertion are true and are interdependent.
Option A is the correct
Note:
You should not fret over finding the value of ‘n’ in Huckle’s rule because ‘n’ is not a characteristic property of any molecule. It is merely a constant which can be substituted with any natural number to satisfy the Huckel's Rule.
Complete step by step answer:
We can identify the and classify compounds as either aromatic or anti-aromatic based on the following rules:
1.For a compound to be Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n+2) \[\pi \]electrons, where ‘n’ denotes the number of subsequent energy levels and can be equal to any whole number, i.e. 0,1,2,3,…
2.And for the compound to be Anti-Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n) \[\pi \]electrons
3.If a compound does not have a continuous ring of conjugated p orbitals in a planar conformation, then it is nonaromatic
One important question you must be having is how we identify \[\pi \]electrons. For that, remember the following points. \[\pi \]electrons lie in p orbitals and \[s{p^2}\]hybridized orbitals, each have 1 p orbital. In a completely conjugated molecule, each carbon atom is \[s{p^2}\]hybridized, and hence the electrons present in these p orbitals are \[\pi \]electrons.
As for the compounds given to us,
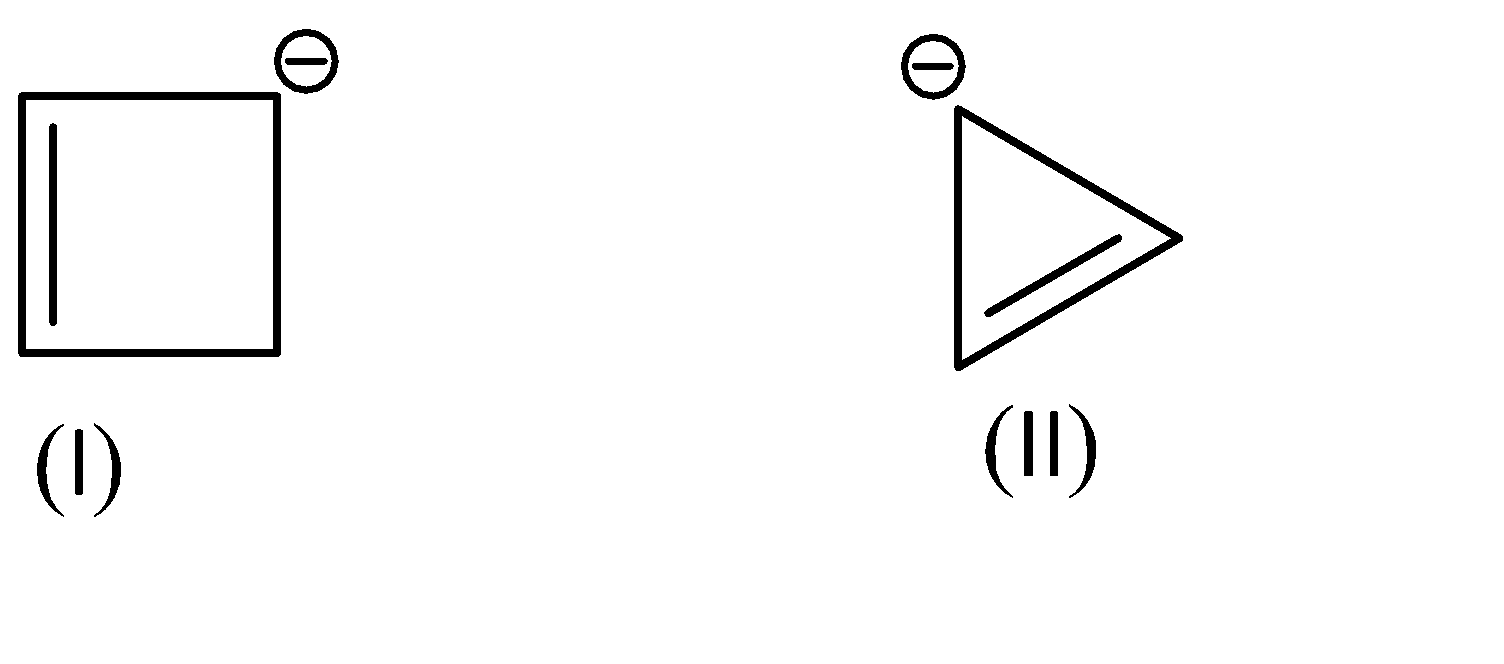
Compound (I) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.But it does not exhibit resonance

Shifting of electrons would bring us back to the same structure.
On the other hand, Compound (II) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.It does exhibit resonance

This compound exhibits resonance in both directions.
And it has 4\[\pi \]electrons, which satisfies Huckle’s rule with the value of n=1.
Hence, we can conclude that Compound (I) is Non-Aromatic and Compound (II) is Anti-Aromatic.
-We know that, the trend in the stability of Aromatic, Non-Aromatic and Anti Aromatic compounds is:
Aromatic > Non-Aromatic > Anti-Aromatic
Hence, Anti aromatic compounds are less stable than Non-aromatic Compounds. This means that the conjugate bases of Anti aromatic compounds are more stable than Non-aromatic Compounds. And we know that the increasing stability of the conjugate base increases the acidity of the compound.
Hence Anti aromatic compounds are less acidic than Non-aromatic Compounds.
\[p{K_a}\] is a method used to indicate the strength of an acid. The lower the value of \[p{K_a}\], higher is the strength of the acid.
Now, relating the above conclusions to the given compounds, we get,
\[p{K_a}\] of Compound(I) < \[p{K_a}\]of Compound (II)
Hence, both the reason and assertion are true and are interdependent.
Option A is the correct
Note:
You should not fret over finding the value of ‘n’ in Huckle’s rule because ‘n’ is not a characteristic property of any molecule. It is merely a constant which can be substituted with any natural number to satisfy the Huckel's Rule.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding the Electric Field of a Uniformly Charged Ring

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Hydrocarbons Class 11 Chemistry Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Chemistry Chapter 5 CBSE Notes - 2025-26

Equilibrium Class 11 Chemistry Chapter 6 CBSE Notes - 2025-26

Organic Chemistry Some Basic Principles And Techniques Class 11 Chemistry Chapter 8 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Chemistry Chapter 7 Redox Reactions (2025-26)




