Question

What is the area of the region enclosed by $y=2|x|$ and $y = 4$?
A. 2 square unit
B. 4 square unit
C. 8 square unit
D. 18 square unit

Answer 1

Hint: To solve this question we are to plot the graph and identify the region enclosed by these
lines. Then, we find the region's coordinates and the region's area.



Formula Used:Area of the triangle = $\dfrac{1}{2} \times$ base $\times$ height
Distance Formula, $d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$



Complete step by step solution:First, we will find the intersection points of the given lines $y=2|x|$and $y = 4$.
Substitute $y = 4$ in the equation, $y=2|x|$.
We get,
$4=2|x|$
$2=|x|$
$x=\pm 2$
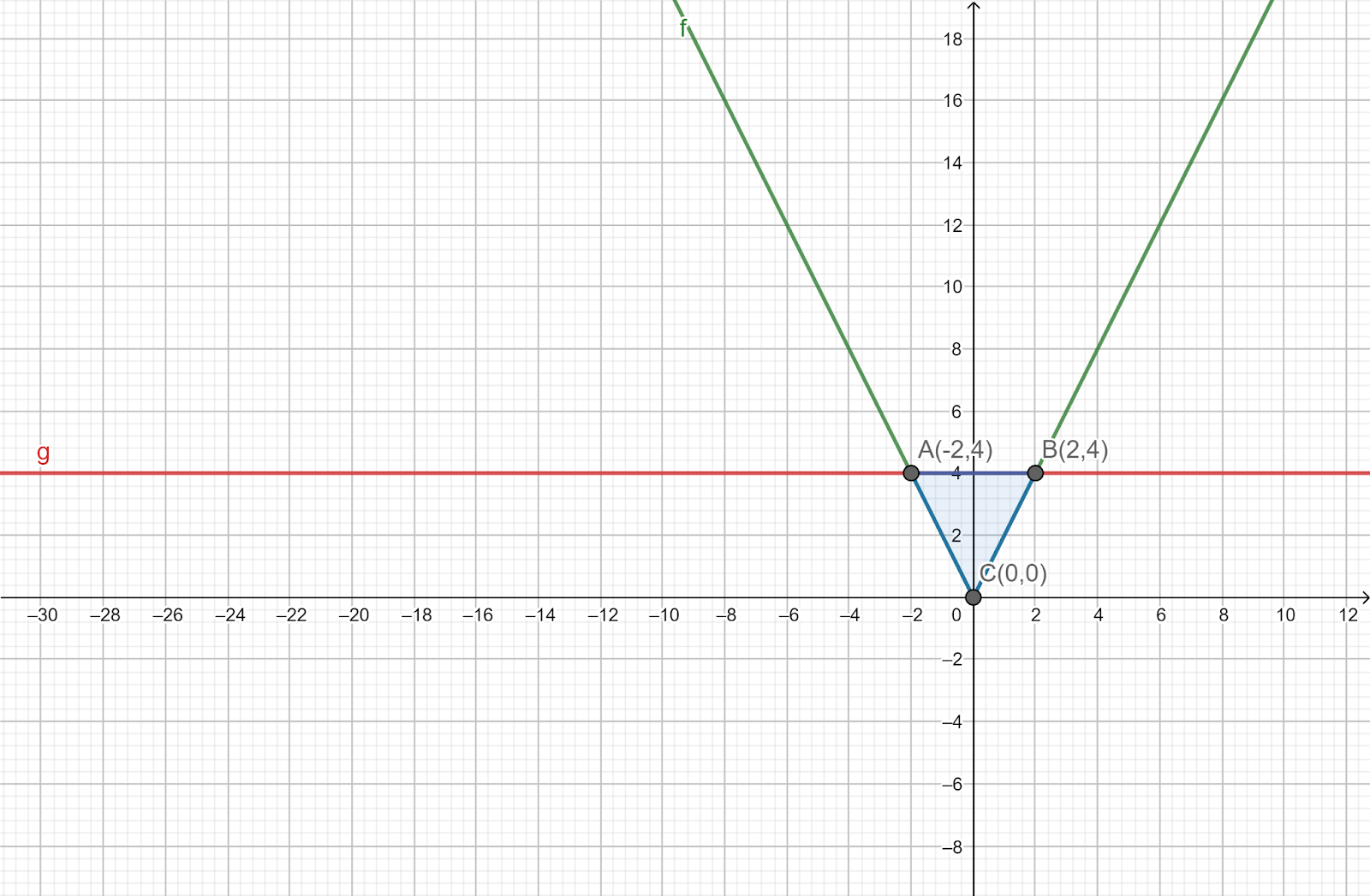
Therefore, the point of intersection is A(-2,4) and B(2,4).
Now, we plot the graph. The region enclosed by the lines is a triangle ABC.

From, the graph we have that the height of the triangle ABC is 4 units. To find the base of the triangle we calculate the distance between points A and B.



We have the distance formula,$d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$
The base of the triangle, AB = $\sqrt{(2-(-2))^{2}+(4-4)^{2}}$
AB = $A B=\sqrt{4^{2}}=4$ units.

Now to find the area of the triangle ABC, we have the formula $\dfrac{1}{2} \times$ base $\times$ height.
Therefore, the area of triangle ABC = \dfrac{1}{2} \times 4 \times 4=8$ square units

The area of the region enclosed by $y=2|x|$and $y = 4$ is 8 square units.



Option ‘C’ is correct

Note: We can find the point of intersection directly from the graph.
- We can also use the method of integration to solve this question. Since the region is symmetric about the x-axis we can find the area of one part and then multiply by 2 to obtain the full area. We have to integrate along the y-axis since the region is bound by the y-axis and the given lines. Now we have to find the function to integrate. We have $y=2x$, then $x=\dfrac{y}{2}$.
Area of the region = $=2 \int_{0}^{4} \frac{y}{2} d y=2\left[\frac{1}{2} \times \frac{y^{2}}{2}\right]_{0=}^{4} \frac{16}{2}=8$ square units.