Question

When you are standing still in rain, you have to hold your umbrella vertically to protect yourself.
(a) When you walk with velocity $90cm/s$ , you have to hold your umbrella at $53^\circ $ above the horizontal. What is the velocity of the raindrops relative to the ground and relative to you?
(b) If we walk with speed $160cm/s$ , how should you hold your umbrella?

Answer 1

Hint If the actual downward velocity of rain be $\overrightarrow v $ and the horizontal velocity of the man be $\overrightarrow u $ , the relative velocity of rain with respect to the man is $w = \sqrt {{v^2} + {u^2}} $ . If the relative velocity makes an angle $\theta $ with the vertical, then, $\tan \theta = \dfrac{u}{v}$ . The relative velocity of raindrops with respect to the person and the speed of the person from the second question will be used to get the angle of the umbrella.
Formula used If the actual downward velocity of rain be $\overrightarrow v $ and the horizontal velocity of the man be $\overrightarrow u $ , the relative velocity of rain with respect to the man is $w = \sqrt {{v^2} + {u^2}} $ .
If the relative velocity makes an angle $\theta $ with the vertical, then, $\tan \theta = \dfrac{u}{v}$ .

Complete step by step answer In the absence of wind, rain falls vertically. But when a man moves forward during a rainfall, he has to hold his umbrella slantingly in front of him. This is due to the fact that the relative velocity of the falling rain with respect to the man makes an angle with the vertical.
Let the actual downward velocity of rain be $\overrightarrow v $ and the horizontal velocity of the man be $\overrightarrow u $ .
Hence, the relative velocity of rain with respect to the man is $\overrightarrow w = \overrightarrow v - \overrightarrow u $ .
$\therefore w = \sqrt {{v^2} + {u^2}} $
If the relative velocity makes an angle $\theta $ with the vertical, then, $\tan \theta = \dfrac{u}{v}$ .
(A) Now, it is given that the velocity of the man, $u = 90cm/s$ and let the actual velocity of rain be $v$ .
Also, the man has to hold his umbrella at $53^\circ $ .

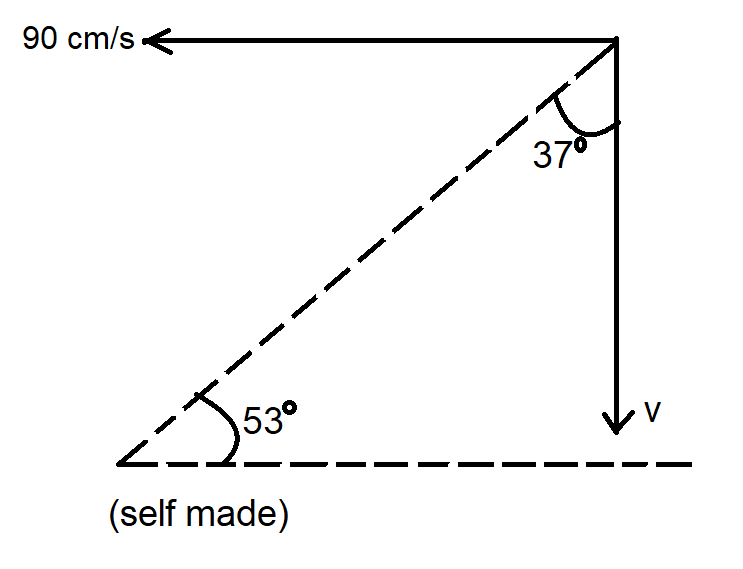
So, according to the formula, we get, $\tan 37^\circ = \dfrac{{90}}{v}$
or, $\dfrac{3}{4} = \dfrac{{90}}{v}$
or, $v = \dfrac{{90 \times 4}}{3} = 120cm/s$
So, the velocity of the raindrops relative to the ground $120cm/s$ .
Now, according to the formula, the relative velocity of rain with respect to the man is
$w = \sqrt {{{\left( {90} \right)}^2} + {{\left( {120} \right)}^2}} = 150cm/s$ .

(B) Now, the velocity of man becomes $160cm/s$ .
Also, we calculated that the relative velocity of rain with respect to the man is $120cm/s$ .
So, $u = 160cm/s$ and $v = 120cm/s$

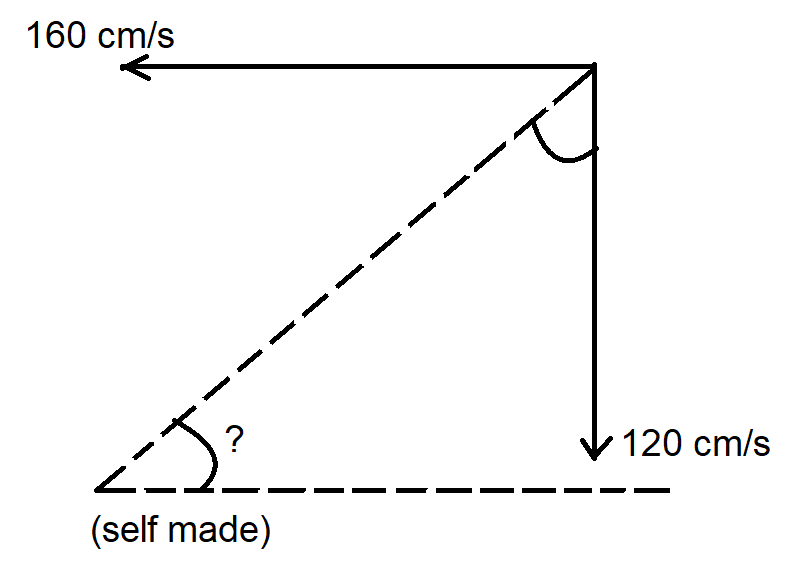
Let, the angle made by the umbrella is $\theta $ .
So, according to the formula, $\tan \theta = \dfrac{u}{v} = \dfrac{{160}}{{120}} = \dfrac{4}{3}$
or, ${\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right) = \theta $
or, $\theta = 53^\circ $
So, the umbrella should be held at $53^\circ $ .

Note As the relative velocity of rain makes an angle with the vertical, it seems that rain comes down at an angle when we move. For the same reason, a speeding vehicle receives more rain on the front wind-screen than on the rear one. Similarly, a person sitting inside a moving train feels that the raindrops follow a slanted path.