Question

An uncharged particle is moving with a velocity of \[\vec v\] in a non-uniform magnetic field as shown. Velocity $\vec v$ would be


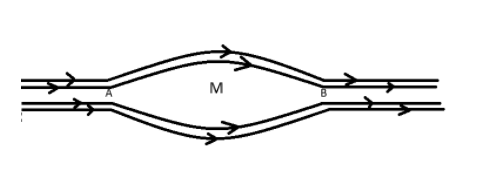
(A) Maximum at $A$ and $B$
(B) Minimum at $A$ and $B$
(C) Maximum at $M$
(D) Same at all points

Answer 1

Hint We are given that the particle is uncharged and also are given with this diagram and we are told that the particle is moving in a magnetic field. Thus, we will take into account the Lorentz force formula which will connect all the given parameters to the required one.
Formula used
${\vec F_L} = q(\vec v \times \vec B)$
Where, ${\vec F_L}$ is the Lorentz force vector, $q$ is the charge on the particle, $\vec v$ is the velocity of the particle and $\vec B$ is the magnetic field in which the particle is moving.

Complete Step By Step Solution
According to Newton’s laws, we know that for a particle to move, there has to be some external force acting on it. Also, we know that for a particle to move in a magnetic field, there has to be a charge on it.
Now,
In this case, the particle is uncharged.
$\therefore q = 0$
Thus from the Lorentz force formula
${\vec F_L} = q(\vec v \times \vec B)$
We can say,
${\vec F_L} = \vec 0$
Thus, there is no Lorentz force acting on the particle at any point in the trajectory.
Also, in accordance to the question, there is no external force acting on the particle.
Thus =, the velocity of the particle $\vec v$ is constant throughout the flow in the given trajectory.

Thus, the answer is (D).

Note The question was about the change in velocity vector of the particle in the three points which we found was the same throughout. But if the question was about the magnetic field change, then the answer would not be the same.