Question

An observer 1.6 m tall is $20 \sqrt{3}$ m away from a tower. The angle of elevation from his eye to the top of the tower is 30°. The height of the tower is
A) 21.6 m
B) 23.2 m
C) 24.72 m
D) None of these

Answer 1

Hint: Use the trigonometric applications involving heights and distances. The distance between the man and the pole is given and the angle of elevation is given. A Trigonometric approach will be the best.

Complete step by step solution:

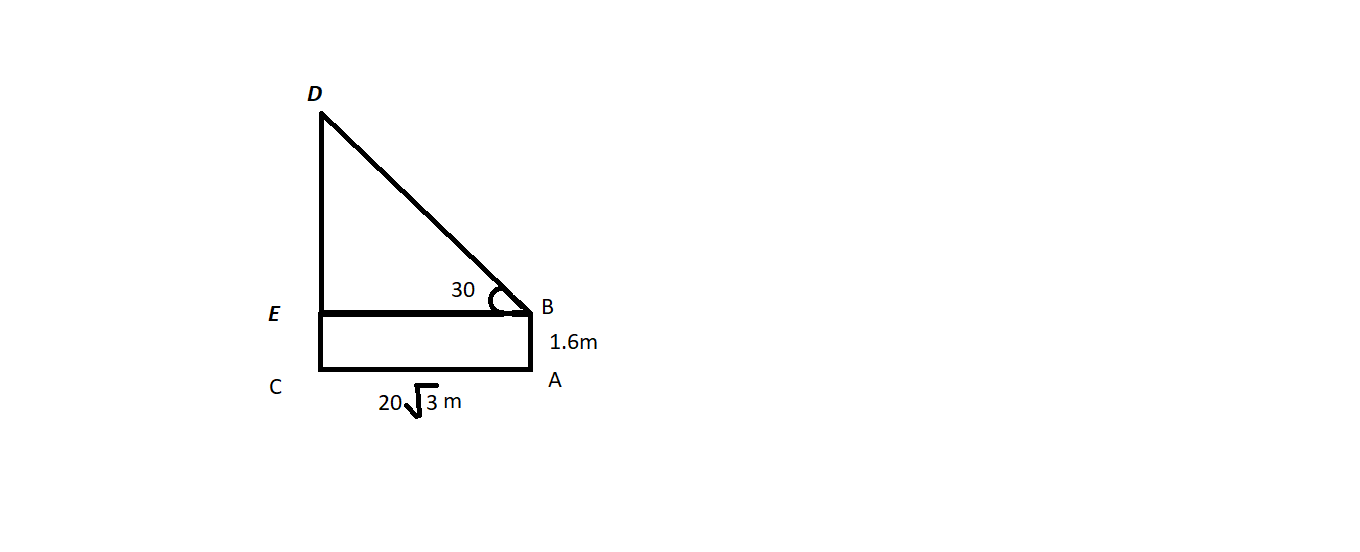
In the above given figure A,
Let $AB$ be the observer and $CD$ tower

Draw $BE$ perpendicular to $CD$
This will represent the distance between the man’s eye and the point E on the pole
Then $CE = AB = 1.6m$
Also,

$BE = AC = 20\sqrt 3 m$
Using the trigonometric applications in the right angled triangle $DEB$
$\tan \theta = \dfrac{P}{B}$
Where, $\theta $is the angle of inclination, $P$ is perpendicular of the triangle and $B$ is the base of the triangle.
Therefore, in triangle $DEB$
$\tan \theta = \dfrac{{DE}}{{BE}}$
Now, we know that
$\tan {30^0} = \dfrac{1}{{\sqrt 3}} $ and
It is given that
$BE = 20\sqrt 3 m$
Putting the values in the above equation, we get,
$\dfrac {1} {{\sqrt 3}} = \dfrac{{DE}}{{20\sqrt 3}} $
Therefore,
$DE = 20m$
Now,
Height of the tower, $CD = DE + CE$
$CD = 20 + 1.6$
$CD = 21.6m$
Therefore, the height of the tower is $21.6m$.

Note: The key application of trigonometry is either to calculate the distance between two or more points or to calculate the height of the object or angle that any object subtends at the specified point without calculating the distance, height or angle actually.