Question

An object $5cm$ tall is placed at a distance of $10cm$ from a concave mirror of radius of curvature $30cm$.
1. Find the nature, position and size of the image.
2. Draw the ray diagram to represent the above case

Answer 1

Hint We are given here with the height of the object, object distance from the mirror and the radius of curvature of the mirror and are also told about the type of mirror. First, we will find the focal length of the mirror as it is defined as half of the radius of curvature. Then we will apply the mirror formula taking into account the sign convention. We will then use the formula for magnification in the mirror to complete the first question. Then using our findings, we will draw a suitable ray diagram.
Formula Used
$f = \dfrac{R}{2}$
Where, $f$ is the focal length of the mirror and $R$ is the radius of curvature of the mirror.
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Where, $v$ is the image distance and $u$ is the object distance from the mirror.
$m = \dfrac{{{h_i}}}{{{h_o}}} = \dfrac{{ - v}}{u}$
Where, $m$ is the magnification by the mirror, ${h_i}$ is the height of the image and ${h_o}$ is the height of the object.

Complete Step By Step Solution
(i)
Here,
Given,
$R = 30cm$
Thus,
Focal length of the mirror, $f = \dfrac{{30}}{2}cm = 15cm$
But the mirror is a concave one.
Thus, the focal length is $f = - 15cm$
Also,
Given,
$u = 10cm$
But it is placed ahead of the mirror.
Thus,
$u = - 10cm$
Now,
We apply the mirror formula,
$\dfrac{1}{{ - 15}} = \dfrac{1}{v} + \dfrac{1}{{ - 10}}$
After further calculations, we get
$v = 30cm$
Thus, the image is formed $30cm$ in behind the mirror.
Now,
For the size and nature of the image, we apply the magnification formula.
$m = \dfrac{{ - 30}}{{ - 10}} = 3$
As the magnification is positive, thus the image formed is virtual and erect and since the value of the magnification is greater than one thus the image is magnified by three times.
Now,
$m = \dfrac{{{h_i}}}{{{h_o}}}$
Putting here the values,
$3 = \dfrac{{{h_i}}}{5} \Rightarrow {h_i} = 15cm$
The size of the image is $15cm$ in height.


(ii)

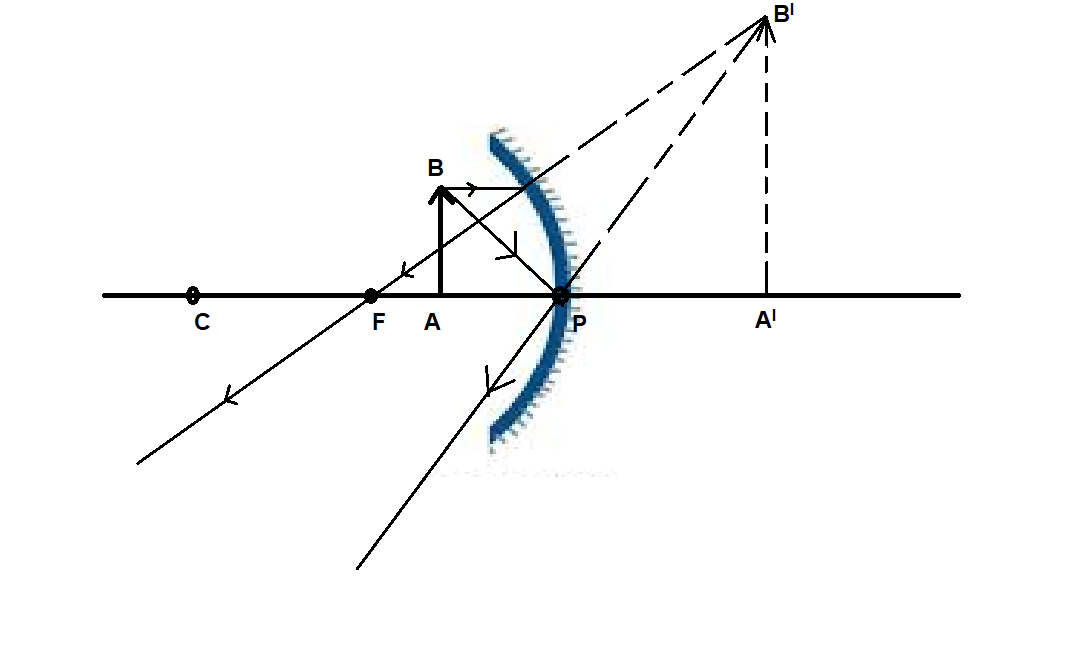
Here,
$AB$ is the object and \[{A^I}{B^I}\] is the image.

Note The mirror was concave thus we took the focal length to be negative. If the mirror was convex, then we should take the focal length as positive and then the whole calculation and the case would be different.