Question

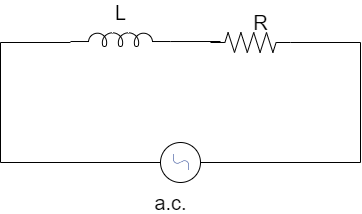
An inductance and a resistance are connected in series with a source of alternating e.m.f. Derive an expression for resultant voltage, impedance and phase difference between current and voltage in alternating circuits.

Answer 1

Hint:The main function of AC source is to alter the supply voltage due to which current and voltages in respective elements of the circuits also changes.

Complete step by step solution:
Step I:
Given that the resistance R and inductance L are connected in series with an alternating e.m.f source. A voltage that varies with time is given by the equation:
$V = {V_0}\sin \omega t$---(i)
Where V is the voltage
t is the time
${V_0}$ is the amplitude and
$\omega $ is the angular frequency

Step II:
Inductance is the amount of voltage generated by an inductor due to movement of charge through the inductor. If at any instant, the current in the circuit be I due to which potential difference across the inductance L can be known using Ohm’s Law.
According to this law
$V = IR$
Where I is the current and R is the resistance
But inductive reactance is the resistance offered to the flow of charge in an a.c. circuit. So the resistance R is equal to $R = {X_L}$
Therefore,
${V_L} = I{X_L}$---(ii)
Where ${X_L}$be the inductive reactance.

Step III:
Similarly potential difference across resistance R is also given by Ohm’s Law
${V_R} = IR$
But $I,{V_R}$are in the same phase

Step IV:
Resultant voltage will be
$V = \sqrt {V_L^2 + V_R^2} $
$V = \sqrt {{{(I{X_L})}^2} + {{(IR)}^2}} $
$V = \sqrt {{I^2}X_L^2 + {I^2}{R^2}} = I\sqrt {X_L^2 + {R^2}} $
$V = I\sqrt {{\omega ^2}{L^2} + {R^2}} $---(iii)

Step V:
Impedance is defined as the total opposition offered to the flow of current in an a.c circuit. It is denoted by symbol Z. It’s formula is
$Z = \dfrac{V}{I}$---(iv)
Substituting the value of V and solving,
$Z = \dfrac{{I\sqrt {{\omega ^2}{L^2} + {R^2}} }}{I} = \sqrt {{\omega ^2}{L^2} + {R^2}} $
Also the value of current can be known by using the formula of equation (iv)
$I = \dfrac{{{V_0}}}{Z}$
$I = \dfrac{{{V_0}}}{{\sqrt {{\omega ^2}{L^2} + {R^2}} }}$

Step VI:
The phase difference is defined as the angular phase difference between the maximum possible value of the two quantities with the same frequency. It is written as
$\tan \Phi = \dfrac{{{V_L}}}{{{V_R}}} = \dfrac{{I{X_L}}}{{IR}}$or
$\tan \Phi = \dfrac{{{X_L}}}{R} = \dfrac{{\omega L}}{R}$
$\Phi = {\tan ^{ - 1}}\dfrac{{\omega L}}{E}$

Note:Sometimes there can be a confusion between resistance and reactance. It is to be remembered that they are different terms. Resistance is the opposition to the flow of current. But reactance is the opposition to the varying current in an inductor.