Question

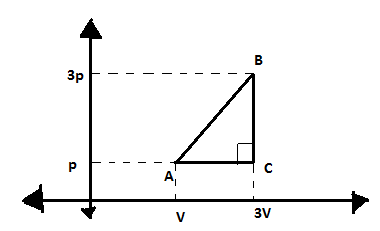
An ideal gas is taken through a process ABCA, as shown in the diagram below. What is the work done in the cycle?

A) $2pV$
B) $pV$
C) $\dfrac{1}{2}pV$
D) zero.

Answer 1

Hint: The work done during a thermodynamic process is known as the thermodynamic work for that system. If the process is depicted on a P-V plane the area under the curve representing the process will be the thermodynamic work for that process.

Complete step by step solution:
For any thermodynamic process if there occurs a change in volume then work is done. Thermodynamic work is the product of constant pressure and the change in volume in an isobaric (constant pressure) process. But for any other process where the volume and pressure change with respect to each other the thermodynamic work done in such a process is equal to the integral of pressure as a function of volume. Mathematically we can write the thermodynamic work done as;
\[W = \int\limits_{{V_1}}^{{V_2}} {P(V)dV} \]
Here, the pressure is a function of volume.
The above equation shows the integral of $PdV$ which means it is the area under the curve.
So we conclude that the thermodynamic work is actually the area of a curve on the P-V plane.
What is a cyclic process?
A cyclic process is a thermodynamic process which has the same initial state and final state. The cyclic process undergoes a process in one direction and then another process comes back to its initial state. On the P-V plane a cyclic process is depicted by a closed figure. Also the area of the closed figure is the thermodynamic work done.
So in this question the process is cyclic. So, the area of the triangle ABC will give us thermodynamic work.
So let us see the coordinates of point A are: $(V,p)$
The coordinates of point B are: $(3V,3p)$
The coordinates of point C are: $(3V,p)$
Thus length of side AC is given by;
$AC = \sqrt {{{(3V - V)}^2} + {{(p - p)}^2}} = 2V$
And length of side BC is given by;
$BC = \sqrt {{{(3V - 3V)}^2} + {{(3p - p)}^2}} = 2p$
Thus the area of the triangle is given by;
$A = \dfrac{1}{2}AC \times BC$
$ \Rightarrow A = \dfrac{1}{2} \times 2V \times 2p$
$\therefore A = 2pV$
Thus the work done in the cyclic process is the area so $2pV$ work is done.

Therefore option A is correct.

Note:You solve the question by integrating all the curves and the finding the equivalent integral of the three integrals.
In other words the region below the triangle will be counted twice so we have to subtract it from the total sum of integrals.