Question

Airspeed of an aeroplane is 400km/hr. The wind is blowing at 200km/hr towards the east direction. In what direction should the pilot try to fly the plane to move exactly towards the northeast.

Answer 1

Hint: When the plane is moving and the wind is blowing due east in this situation when the plane steers towards northeast then the effect of wind blowing will also affect the angle turned by the aeroplane it will turn more than it was steered to turn. So, if we want to steer at a particular angle then we need to steer at an angle lower than desired because the rest of the turn will be due to the effect of wind.

Complete step by step solution:
Consider the following diagram in this case: the plane is flying and the wind is blowing due east. Now here it is said that the plane needs to be steered exactly northeast. Now as we can see that the exact northeast will be at \[45^\circ \].
So if we need to travel at \[45^\circ \] we will take a steer at an angle more than \[45^\circ \] so the wind will show its effect and the resultant of wind and aeroplane will be at \[45^\circ \].

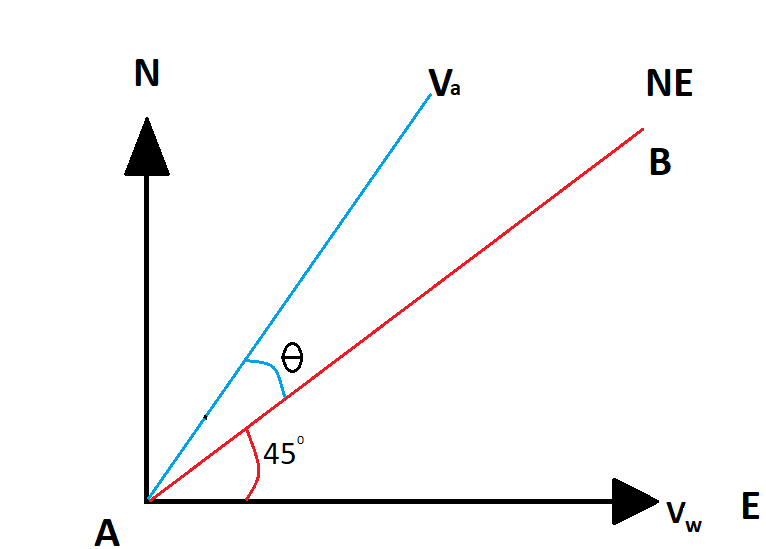
Now in this figure, the red line is the actual path the plane needs to turn and the blue line is the path we will turn to compensate for the effect of wind blowing due east.

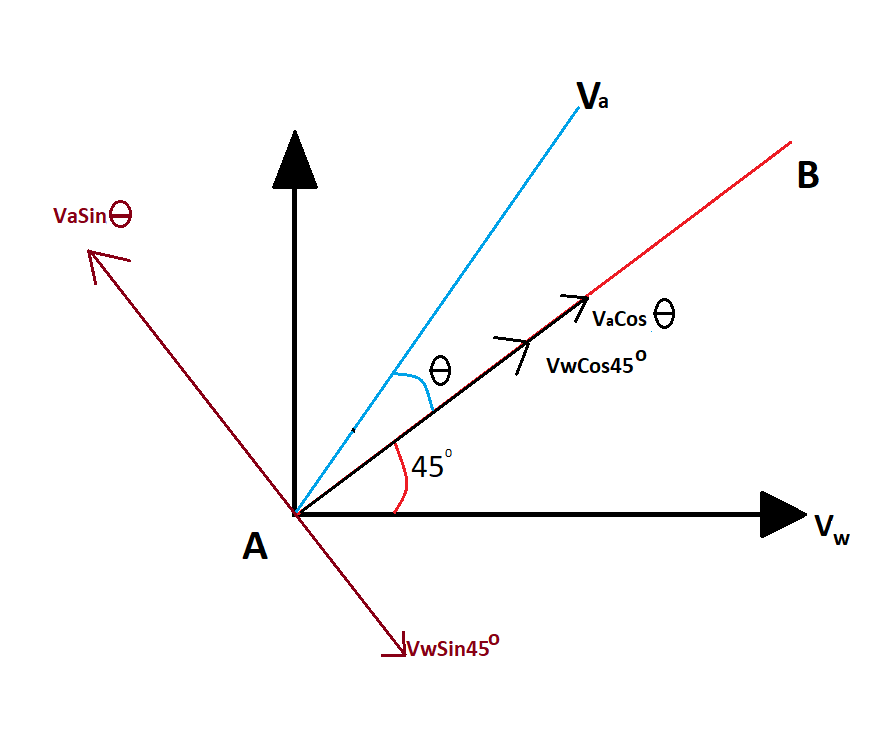
Now resolving the components of ${V_a}$ we get ${V_a}\operatorname{Cos} \theta $ along AB.
And ${V_a}\operatorname{Sin} \theta $ perpendicular to AB
Similarly,
Now we will resolve ${V_w}$ for AB
So, we will get ${V_w}\operatorname{Cos} 45^\circ $ along AB
And ${V_w}\operatorname{Sin} 45^\circ $ perpendicular to that
Now in the figure, we can see that the components ${V_a}\operatorname{Cos} \theta $ and ${V_a}\operatorname{Cos} 45^\circ $ will steer the plane along with AB
And ${V_w}\operatorname{Sin} 45^\circ $, ${V_a}\operatorname{Sin} \theta $ acting in opposite directions will be equal and cancel out each other.
So the net resultant force will be along AB and plane will steer exactly at $45^\circ $
On equating we get ${V_a}\operatorname{Sin} \theta = {V_w}\operatorname{Sin} 45^\circ $
Substituting the values, we get
${V_a}$ is the velocity of the aeroplane $ = 400m{s^{ - 1}}$
${V_w}$ is the velocity of the wind $ = 200m{s^{ - 1}}$
$\Rightarrow 400\operatorname{Sin} \theta = 200\operatorname{Sin} 45^\circ $
$\Rightarrow \operatorname{Sin} \theta = \dfrac{{200}}{{400}}\operatorname{Sin} 45^\circ $
$ \Rightarrow \operatorname{Sin} \theta = \dfrac{1}{2}\operatorname{Sin} 45^\circ $
$ \Rightarrow \theta = 20.70^\circ $
Final answer: The pilot needs to turn an angle of $20.70^\circ $ to move exactly northeast.

Note: The resultant of both the motion will give us the actual motion.
When a plane is flying and it takes a turn and there is wind flowing then the effect of the wind will also be considered in steering the plane.
The effect of wind generally increases or decreases the angle the pilot needs to steer the plan to get into a particular direction.