Question

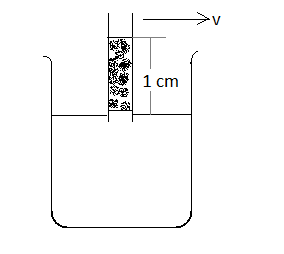
When air density \[1.3kg {m^ {- 3}}\] flows across the top of the lobe shown in the accompanying figure, water rises in the lobe to a height of $1.0cm$ . What is the speed of the air? V is the velocity of the water at the height of 1 cm.

Answer 1

Hint: The theory of work and kinetic energy (also known as the work-energy theorem) states that the work performed by the sum of all forces acting on a particle equals the difference in the kinetic energy of the particle. This description can be generalised to solid bodies by describing the work of the torque and rotational kinetic energy.

Complete step by step solution:
The work / energy hypothesis describes the principle that network work – the entire work carried out by all the forces together – on a single object is the same as change in the object's kinetic energy. Since eliminating the net force (no further work is performed), the cumulative energy of the object is changed due to the work done.

Work moves energy from place to place or from form to form. The work will alter the potential energy in a mechanical device, the heat energy in a thermal system, or electrical energy in an electrical device, in more general systems than those described here.
The kinetic energy generated due to velocity will be equal to the potential energy generated in the lobe.
Kinetic energy due to velocity $v$ will be,
$\dfrac {1} {2} {\rho _ {air}} {v^2} $
${\rho _ {air}} $ is the density of air.
$v$ is the velocity.
Potential energy in the lobe is,
${\rho _w} g {h_w} $
Where, the density of the water is ${\rho _w} $, $g$ is acceleration due to gravity, ${h_w} $ is the height of water in the lobe.
Now, according to work energy theorem,
$\dfrac {1} {2} {\rho _ {air}} {v^2} = {\rho _w} g {h_w} $
$ \Rightarrow v = \sqrt {\dfrac{{2{\rho _w} g {h_w}}} {{{\rho _ {air}}}}} $
$ \Rightarrow v = \sqrt {\dfrac{{2 \times {{10} ^3} \times 10 \times {{10} ^ {- 2}}}} {{1.3}}} $
$v = 12.4m{s^ {- 1}} $

The speed of air is $12.4m{s^ {- 1}} $.

Note: The loss in kinetic energy, on the other hand, results through an equal number of negative work carried out by the resulting force. Therefore, if the network is positive, the kinetic energy of the particle will increase by the work. If the network work carried out is negative, the cinematic energy of the particles lowers the workload. Work is the energy associated with force action, and work then has the spatial and unitary components of energy.