Question

Acceleration of a particle, executing SHM, at its mean position is
(A) Infinity
(B) Varies
(C) Maximum
(D) Zero

Answer 1

Hint: The restoring force works in the opposite direction of the displacement and is inversely proportional to the particle's displacement from its mean position. The mass times the acceleration product also equals this force. The particle's displacement is zero at mean position.

Complete answer:
Simple harmonic motion is when a particle oscillates up and down (back and forth) about a mean position (also known as equilibrium position) in such a way that a restoring force/ torque acts on the particle, which is proportional to displacement from mean position but acts in the opposite direction from displacement. It is known as a linear S.H.M. if the displacement is linear, and an angular S.H.M. if the displacement is angular.
Example:
1) a body suspended by a spring moving
2) Simple pendulum oscillations

Acceleration of a particles:
In S.H.M., a particle's acceleration is given by $a=\dfrac{dv}{dt}=-{{\omega }^{2}}A\sin (\omega t+\phi )$or $a=-{{\omega }^{2}}y$.
The acceleration is pointed toward the mean position, as shown by the negative sign
${{a}_{\max }}=-{{\omega }^{2}}A$ when$y=A$ (at an extreme position).

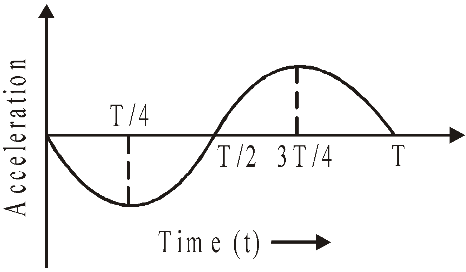
When undergoing SHM, a particle will accelerate as it approaches the mean position before decelerating till it reaches its end locations. As a result, the net acceleration is constant at zero.

So, the correct option is D.

Note: SHM has a total energy of $1/2M{{\omega }^{2}}{{A}^{2}}$. Equation $a=-{{\omega }^{2}}y$ demonstrates that if a body performs a S.H.M., its acceleration will be proportional to its displacement but will be in the opposite direction. Any motion must meet this crucial criteria in order to be valid.