Question

ABCD is a rectangular field. A vertical lamp post of height 12 m stands at the corner A. If the angle of elevation of its top from B is 60° and from C is 45°. then the area of the field is
A. $48\sqrt{2\,}$sq m
B. $48\sqrt{3}$ sq m
C. $12\sqrt{3}$sq m
D. $12\sqrt{2}$sq m

Answer 1

Hint:
We use Pythagoras theorem to solve this question. The well-known Pythagorean Theorem states that the square on the hypotenuse of a right triangle equals the sum of the squares on its legs. First we find the values of AB and AC by using simple trigonometric functions. Then by using Pythagoras theorem we find the value of BC and after that we are able to find the area of the field.

Formula Used:
The formula for the Pythagoras theorem is written as $H^{2}=P^{2}+B^{2}$, where
$H^{2}$ is the hypotenuse of the right triangle
and $P$ and $B$ are its other two legs

Complete Step by step Solution:
Let EA be the lamppost at corner A and ABCD be the rectangular field.

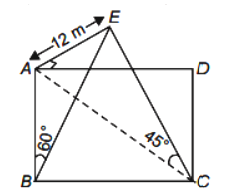
Since AE is a vertical pole, all lines in the planes of the rectangular grid are perpendicular to it, i.e., EA is perp. to AB, BC, CD, and DA.
$\therefore \angle \mathrm{EAD}=90^{\circ}$
Given,
$E A=12 \mathrm{~m}$
Join E B, E C, and A C
Also Given that
$\angle \mathrm{EBA}=60^{\circ}, \angle \mathrm{ACE}=45^{\circ} .$
In . $\triangle A B E$,
$\tan 60^{\circ}=\dfrac{A E}{A B}=\dfrac{12}{A B}$
$\Rightarrow \sqrt{3}=\dfrac{12}{A B}$
$\Rightarrow A B=\dfrac{12}{\sqrt{3}}=4 \sqrt{3} \mathrm{~m}$
In $\triangle$ ACE,
$\tan 45^{\circ}=\dfrac{A E}{A C}$
$\Rightarrow \dfrac{12}{A C}=1$
$\Rightarrow A C=12 \mathrm{~m}$
In $\triangle A B C$,
According to the Pythagoras theorem
$\mathrm{BC}=\sqrt{A C^{2}-A B^{2}}$
$=\sqrt{144-48}$
$=\sqrt{96} \mathrm{~m}$
$=4 \sqrt{6} \mathrm{~m}$
Area of the rectangular field $=\mathrm{AB} \times \mathrm{BC}$
$=4 \sqrt{3} \times 4 \sqrt{6}$
$=48 \sqrt{2}$ sq. $\mathrm{m}$
So the correct answer is option A.

Note: The formula for the Pythagoras theorem is written as $H^{2}=P^{2}+B^{2}$, where $H^{2}$ is the hypotenuse of the right triangle and $P$ and $B$ are its other two legs. As a result, the Pythagoras equation can be used to any triangle that has one angle that is exactly 90 degrees to create a Pythagoras triangle.