Question

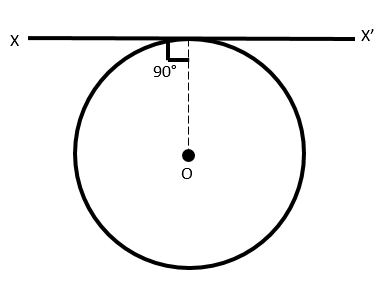
A wire of length L and uniform mass density \[\rho \] is bent into a circular loop with center at O as shown. The moment of inertia of the loop about the axis XX’ is:

A. \[\dfrac{{\rho {L^3}}}{{8{\pi ^2}}} \\ \]
B. \[\dfrac{{\rho {L^3}}}{{16{\pi ^2}}} \\ \]
C. \[\dfrac{{5\rho {L^3}}}{{16{\pi ^2}}} \\ \]
D. \[\dfrac{{3\rho {L^3}}}{{8{\pi ^2}}}\]

Answer 1

Hint:To find the moment of inertia of a body about an axis parallel to another axis of rotation when the moment of inertia about the known axis of rotation is known, we use the parallel axis theorem.

Formula used:
\[I = {I_{cm}} + m{d^2}\]
Here, I is the moment inertia about the required axis of rotation, \[{I_{cm}}\] is the moment of inertia of about center of mass, m is the mass of the body and d is the distance of the required axis of rotation from the center of mass.
The moment of inertia of circular loop of mass m and radius r about diameter is given as,
\[{I_O} = \dfrac{{m{r^2}}}{2}\],
Here m is the mass of the loop and r is the radius of the loop.

Complete step by step solution:
The given axis of rotation XX’ is parallel to the diameter of the loop.

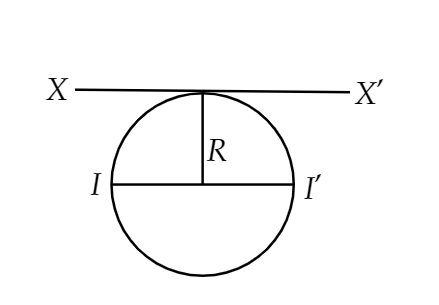
Image: Wire of length L in circular form

The distance of the axis of rotation from the center of mass is \[d = r\]
The moment of inertia of the circular loop about the diameter is \[{I_{cm}} = \dfrac{{m{r^2}}}{2}\]
The mass of the circular loop of length L having linear mass density \[\rho \]is,
\[m = \rho L\]
If the radius of the circular loop is r then the circumference of the loop will be equal to the total length of loop, i.e. L.
\[2\pi r = L \Rightarrow r = \dfrac{L}{{2\pi }}\]

Putting in the expression for the moment of inertia about the axis of rotation XX’, we get
\[{I_{XX'}} = {I_{cm}} + m{d^2}\]
\[\Rightarrow {I_{XX'}} = \dfrac{{\rho L{{\left( {\dfrac{L}{{2\pi }}} \right)}^2}}}{2} + \rho L{\left( {\dfrac{L}{{2\pi }}} \right)^2}\]
\[{I_{XX'}} = \dfrac{{\rho {L^3}}}{{8{\pi ^2}}} + \dfrac{{\rho {L^3}}}{{4{\pi ^2}}}\]
\[\therefore {I_{XX'}} = \dfrac{{\rho {L^3} + 2\rho {L^3}}}{{8{\pi ^2}}} = \dfrac{{3\rho {L^3}}}{{8{\pi ^2}}}\]
Hence, the moment of inertia of the given circular loop about the axis of rotation XX’ is \[\dfrac{{3\rho {L^3}}}{{8{\pi ^2}}}\].

Therefore, the correct option is D.

Note: The moment of inertia of the circular loop about the diameter is calculated using perpendicular axis theorem. The perpendicular axis theorem is applied where the mass distribution is uniform along the plane of the body.