Question

A voltmeter and an ammeter are connected in series to an ideal cell of emf $E$.The voltmeter reading is $V$and the ammeter reading is $I$, then:
 i. $V < E$
ii. The voltmeter resistance is $\dfrac{V}{I}$.
iii.The potential difference across the ammeter is $E - V$.
iv. Voltmeter resistance plus ammeter resistance $ = \dfrac{E}{I}$.
The correct statements are:
(A) i and ii
(B) ii and iii
(C) iii and
(D) all

Answer 1

Hint: First draw the circuit diagram and then use KVL to solve the sum.
Electromotive force is defined as the electric potential produced by changing the magnetic field. It is independent of circuit resistance.
Voltmeter is an instrument used for measuring the voltage and ammeter is an instrument used for measuring the current.
Here the cells are connected in series so current flows through each cell.

Complete step by step answer: Let us draw a circuit diagram for solving the given question.
   
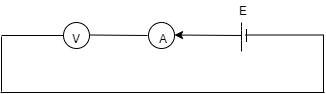
The current$(I)$ is flowing from the positive terminal of the ideal cell to the negative terminal. It is said that the cell is ideal so it has negligible internal resistance. On the other hand, the voltmeter and ammeter are not ideal so they will have internal resistances.
Let ${r_V}$and ${r_A}$be the internal resistances of the voltmeter and ammeter respectively.
Now we will check which of the given statements are correct.
The first statement says that $V < E$. To check this, we apply Kirchhoff’s Voltage law and get the following relation:
$E - I{r_A} - I{r_V} = 0$ $eqn.1$
$ \Rightarrow E = I{r_A} + I{r_V}$
$ \Rightarrow E = {V_A} + V$ $eqn.2$
 where ${V_A}$is the voltage drop across ammeter and $V$is the voltage drop across the voltmeter or the reading of the voltmeter.
As, $E$is a summation of ${V_A}$and $V$so, it is clear that $V < E$. Thus, the first statement is correct.
The second statement states that the voltmeter resistance is $\dfrac{V}{I}$.This statement is the mathematical representation of Ohm’s law. So, the second statement is correct.
If we refer to $eqn.2$ we get, ${V_A} = E - V$ , where ${V_A}$is the voltage drop or the potential difference across ammeter . So, the third statement that says the potential difference across the ammeter is $E - V$is correct.
From $eqn.1$we get,
$I{r_A} + I{r_V} = E$
$ \Rightarrow \left( {{r_A} + {r_V}} \right) = \dfrac{E}{I}$
Thus, it is correctly stated in the fourth statement that Voltmeter resistance plus ammeter resistance $ = \dfrac{E}{I}$.

Since all the statements are correct, option D is the correct answer to the question.

Note: Kirchhoff’s voltage law states that the sum of all the voltage in a circuit loop is zero. One of the main disadvantages of connecting the cells in series is that if one component of circuit fails then all the components in the circuits will fail and another disadvantage is that as the number of components in the circuits increases the net resistance of the circuit will also increase.