Question

A uniform solid cylinder of density $0.8{\text{gc}}{{\text{m}}^{ - 3}}$ floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical. The densities of liquids A and B are $0.7{\text{gc}}{{\text{m}}^{ - 3}}$ and $1.2{\text{gc}}{{\text{m}}^{ - 3}}$ , respectively. The height of liquid A is ${h_A} = 1 . 2{\text{cm}}$ . The length of the part of the cylinder with liquid B is ${h_B} = 0 . 8{\text{cm}}$ and $h = 0.2{\text{cm}}$ . Find the total force exerted by liquid A on the cylinder.

Answer 1

Hint: Here the cylinder is mentioned to be in equilibrium as it floats in the combination of the two liquids A and B. Liquid A and liquid B will exert pressure on the sides of the cylinder. The total force acting on the cylinder by liquid A will be the product of the total exerted pressure by liquid A and the area of the cylinder present in liquid A.

Formula used:
The force acting on an object in a fluid is given by, $F = PA$ where $P$ is the pressure exerted by the fluid on the object and $A$ is the area of the object.

Complete step by step answer:
Step 1: Sketch the given figure and list the given parameters.
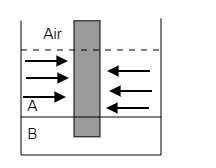
The figure given below represents the cylinder placed in the combination of two liquids A and B.
The density of liquids A is given to be ${\rho _A} = 0.7{\text{gc}}{{\text{m}}^{ - 3}}$ and that of liquid B is given to be ${\rho _B} = 1.2{\text{gc}}{{\text{m}}^{ - 3}}$ .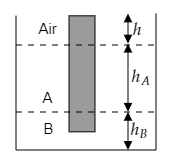
The density of the solid cylinder is given to be ${\rho _{cylinder}} = 0.8{\text{gc}}{{\text{m}}^{ - 3}}$ .
The length of the cylinder present in liquid A is given to be ${h_A} = 1.2{\text{cm}}$ .
The length of the cylinder present in liquid B is given to be ${h_B} = 0.8{\text{cm}}$ .
The length of the cylinder present in the air is given to be $h = 0.2{\text{cm}}$.

Step 2: Express the pressure exerted on the cylinder by liquid A.
Liquid A will exert pressure on both sides of the cylinder to keep it in equilibrium. Then the pressure exerted on one side will be cancelled by the pressure exerted by the liquid on the other side. The arrows in the figure below represent the pressure exerted on the sides of the cylinder by liquid A.

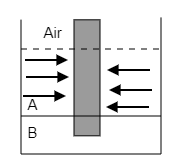
So the net pressure exerted on the cylinder by liquid A will be zero i.e., ${P_A} = 0$ .
If ${A_A}$ is the area of the cylinder present in liquid A then the force exerted by liquid A on the cylinder can be expressed as ${F_A} = {P_A}{A_A}$ ------- (1)
Substituting ${P_A} = 0$ in equation (1) we get, ${F_A} = 0 \times {A_A} = 0$

Thus the total force exerted by liquid A on the cylinder is obtained to be zero.

Note: The magnitude of the forces exerted on the individual sides of the given cylinder will not be zero. But the forces will be opposite in direction and hence the total force exerted by liquid A will be zero. This is because the cylinder is mentioned to be in equilibrium. The given values are not needed to determine this total force exerted on the cylinder.