Question

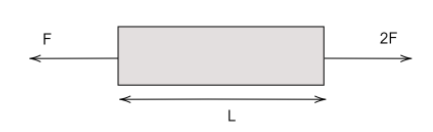
A uniform rod (area of cross-section $A$, Young’s Modulus $Y$, Length $L$, mass $M$) is pulled on a smooth horizontal surface as shown. Calculate the elongation of the rod after a long time.

Answer 1

Hint: When a body is moved in a way that it experiences a force from both directions, it moves in a direction where the force is greater in magnitude. But due to the presence of other forces, stress is developed in the body and this causes it to either shrink or elongate by some amount, this change in the length can be calculated using the young’s modulus- which is the ratio of stress to strain.

Complete step by step solution:
Stress $(\sigma )$ is the number of internal forces produced as a reaction to an external force and maintains the shape of a body intact. Stress in a body is equal to the amount of force applied to the body from both ends. It is given by the formula-
$\sigma = \dfrac{F}{A}$
where $F$ is the amount of force that is applied and $A$ is the area over which this force acts.
Strain$(\varepsilon )$ is defined as the amount of deformation that occurs due to an external force and can be defined as the ratio of change in dimensions to the original dimension of the body. For a rod, this change is the change in length. Therefore,
$\varepsilon = \dfrac{{\Delta L}}{L}$
The Young’s modulus is defined as the ratio of the stress applied in a body to the strain produced due to it.
$Y = \dfrac{\sigma }{\varepsilon }$
$ \Rightarrow Y = \dfrac{{FL}}{{A\Delta L}}$
For the given rod, the acceleration is given by-
$a = \dfrac{F}{M}$
As the rod moves due to this acceleration, the amount of stress changes linearly, which is maximum at the point where force is applied and reduces as the distance increases.
Consider a small length $\;dx$ at a distance of $x$ from the free end of the rod. Then,
$F' = \dfrac{{Fx}}{L}$
The stress in this case is,
$\sigma = \dfrac{{F'}}{L}$
$ \Rightarrow \sigma = \dfrac{{Fx}}{L}$
Thus the elongation of the rod in this differential element is-
$d\Delta L = \varepsilon L$
$d\Delta L = \dfrac{{\varepsilon F}}{{A\sigma L}}xdx$
Integrating this equation,
$\int\limits_0^{\Delta L} {d\Delta L} = \int\limits_0^L {\dfrac{{\varepsilon F}}{{A\sigma L}}xdx} $
Pushing the constants out of the integration function,
$\int\limits_0^{\Delta L} {\Delta L} = \dfrac{F}{{YAL}}\int\limits_0^L {xdx} $
Upon evaluating the limits of the integration we get,
$\left[ {\Delta L} \right]_0^{\Delta L} = \dfrac{F}{{YAL}}\left[ {\dfrac{{{x^2}}}{2}} \right]_0^L$
$\Delta L = \dfrac{{FL}}{{2YA}}$

The elongation produced in the rod is $\Delta L = \dfrac{{FL}}{{2YA}}$

Note: The rod gets elongated because the direction of the forces acting on it is tensile, if the forces were compressive the rod would have shrunk by the same amount. Also, due to an imbalance of forces on both sides, it would then move in the opposite direction.