Question

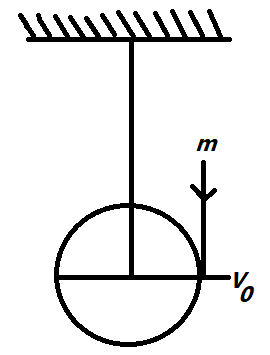
A uniform disc of mass M and radius R is hanging from a rigid support and is free to rotate about a horizontal axis passing through its centre in the vertical plane as shown. An insect of mass m falls vertically and hits the disc at a point at horizontal diameter with a velocity ${v_0}$ and sticks on it. Calculate the minimum value of ${v_0}$ so that the disk completes the vertical circular motion.

Answer 1

Hint: Here in this question, we have to find the minimum value of the velocity by which the disk completes the vertical circular motion. To find this, we must know about conserving angular momentum. A spinning system's ability to conserve angular momentum ensures that its spin will not change until it is subjected to an external torque and in other words the rotation's speed will not change as long as the net torque is zero.

Formula used:
According to conservation of angular momentum,
$m{v_0}R = \left( {\dfrac{{M{R^2}}}{2} + m{R^2}} \right)\omega $
Here, $m$ is the mass of the insect, $v_0$ is insect velocity, $M$ is the mass of the disc and $R$ is its radius and $\omega$ is the angular velocity.

Complete step by step solution:
We know that preserving the system's overall angular momentum around the disc's centre of mass,
$m{v_0}R = \left( {\dfrac{{M{R^2}}}{2} + m{R^2}} \right)\omega $
Here we need the value of omega, so taking omega one side and getting the value of it,
$\omega = \dfrac{{2m{v_0}}}{{(M + 2m)R}} .....(i) \\ $
After which taking conservation of energy we get,
$mgR = \dfrac{1}{2}\left( {\dfrac{{M{R^2}}}{2} + m{R^2}} \right){\omega ^2}.....(ii) \\ $
By putting the value of $\omega $ from equation(i) to equation(ii) we get the final value as,
$mgR = \dfrac{1}{2}\left( {\dfrac{{M{R^2}}}{2} + m{R^2}} \right)\left( {\dfrac{{2m{v_0}}}{{(M + 2m)R}}} \right) \\ $
Here in the above equation, we need the value of velocity ${v_0}$ , so by finding velocity we get the value as,
${v_0} = \sqrt {\dfrac{{\left( {M + 2m} \right)gR}}{m}} $
Here in the above equation, we get the final value of velocity.

Therefore, the minimum value of the velocity by which the disk completes the vertical circular motion is ${v_0} = \sqrt {\dfrac{{\left( {M + 2m} \right)gR}}{m}}$.

Note: When a body moves in a vertical circle so that its motion at various points varies, the movement is referred to as vertical circular motion. Consider a massed object that is tethered to one end of an infinitely long, extendable string and rotated in a vertical arc of radius r.