Question

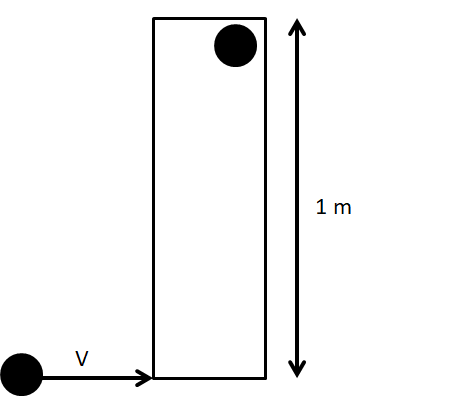
A thin rod of mass \[\;0.9kg,\] and length \[1{\text{ }}m\] is suspended, at rest, from one end so that it can freely oscillate in the vertical plane. A particle of mass \[0.1{\text{ }}kg\] moving in a straight line with velocity \[80{\text{ }}m/s\] hits the rod at its bottom most point and sticks to it (see figure). The angular speed \[\left( {in{\text{ }}rad/s} \right)\] of the rod immediately after the collision will be __________.

Answer 1

Hint: We can say that to determine the angular speed of a body, we need to apply the conservation of angular momentum to it. Here, the kinematics of the oscillation mode are governed by the equation. We have to use the given figure for the reference.

Complete step by step solution:
The rod of mass \[0.9{\text{ }}kg\] and length \[1{\text{ }}m\] is suspended, at rest, from one end so that it can freely oscillate in the vertical plane. We know that when an object is touching a flat surface, there are no stresses on the surface. This means that the surface will not transmit any forces to the object below it but allow free sliding.

The mass of the rod is\[\;0.9kg,\] the length of the rod is \[1m\], the mass of the particle is \[0.1kg\], and the particle's velocity is \[20\,rad/s\]. To Determine: The rod's angular speed. When the particle collides with the rod, make a schematic diagram. Before and after the collision, use the conservation of angular momentum. Find the angular speed of the rod by substituting the supplied value into the equation \[mbv = \left( {m{L^3}/3{\text{ }} + mp{L^2}} \right)\]

Applying COAM about the Pivot,
\[\begin{array}{*{20}{l}} {{L_i}\; = {\text{ }}{L_f}} \\ \Rightarrow {0.1{\text{ }} \times {\text{ }}80{\text{ }} \times {\text{ }}1{\text{ }} = {\text{ }}\{ [0.9{\text{ }} \times {\text{ }}{1^2}]{\text{ }}/{\text{ }}3\} {\text{ }} \times {\text{ }}\omega {\text{ }} + {\text{ }}\left( {0.1} \right){\text{ }}{1^2}\;\omega } \\ \Rightarrow {8{\text{ }} = {\text{ }}\left( {0.3{\text{ }} + {\text{ }}0.1} \right){\text{ }}\omega } \\ \Rightarrow {8{\text{ }} = {\text{ }}\left( {0.4} \right){\text{ }}\omega } \\ \therefore {\omega {\text{ }} = {\text{ }}80{\text{ }}/{\text{ }}4{\text{ }} = {\text{ }}20} \end{array}\]

The angular speed is \[20\,rad/s\].

Note: This case is about a thin rod at rest and oscillating horizontally. The thin rod could be either in equilibrium or unstable. In equilibrium, the force on the rod must be zero so that it would not accelerate. But if the force on one end of this thin rod was stronger than that on the other, then it will accelerate and move to a point where force is zero. On instability, it will oscillate back and forth between these two points with a constant acceleration.