Question

A straight rod of length L extends from x=a to =L+a. The gravitational force is exerted on a point mass ‘m’ at x=0, if the mass per unit length of the rod is $A+B{{x}^{2}}$ is given by:
A. $\text{A}\text{. }Gm\left[ A\left( \dfrac{1}{a+L}-\dfrac{1}{a} \right)-BL \right]$
B. $\text{B}\text{. }Gm\left[ A\left( \dfrac{1}{a}-\dfrac{1}{a+L} \right)+BL \right]$
C. $\text{C}\text{. }Gm\left[ A\left( \dfrac{1}{a+L}-\dfrac{1}{a} \right)+BL \right]$
D. $\text{D}\text{. }Gm\left[ A\left( \dfrac{1}{a}-\dfrac{1}{a+L} \right)-BL \right]$

Answer 1

Hint: Consider a dm mass of dx length of the rod, whose distance from the point mass is x. Then find the force (dF) exerted on the point mass by this dm mass by the law of gravitation (i.e. $F=\dfrac{G{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}$). Use the value of the mass per unit length given and find the relation between dm and dx. Then integrate dF for the limits from x=a to x=a+L.

Formula used:
$F=\dfrac{G{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}$

Complete step by step answer:
Let us first draw a figure from the given data for better understanding of the question. It is given that there is a rod of length L. Let the rod be on the x-axis and be positioned between x = a and x = L + a. Let the point mass ‘m’ be placed at the origin (i.e. x=0), as shown in the figure.



It is asked to find the gravitational force exerted by the rod on the point mass.
We can first find what the force exerted by a small element of the rod is and then integrate the force for the whole rod.
Therefore, consider a small element of the rod, whose mass is dm and length is dx. Let the distance of this element from the point mass (at x = 0) be x, as shown below.



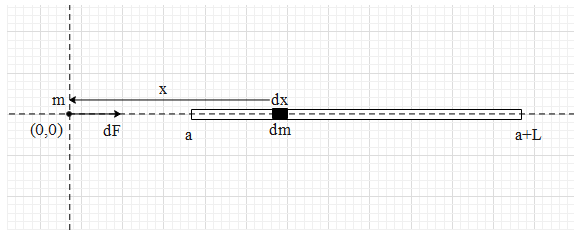
Now according to the law of gravitation, the dm mass will exert a force on the point mass m whose magnitude will be equal to $dF=\dfrac{Gmdm}{{{x}^{2}}}$ …… (i).
The direction of the force dF will be towards the dm mass (always an attractive force).
Now, it is given that the mass per unit length of the rod is $A+B{{x}^{2}}$.
Therefore, $\dfrac{dm}{dx}=A+B{{x}^{2}}$
$\Rightarrow dm=\left( A+B{{x}^{2}} \right)dx$
Substitute the value of dm in equation (i).
$dF=\dfrac{Gm\left( A+B{{x}^{2}} \right)dx}{{{x}^{2}}}$ …… (ii).
This is the force exerted on the point mass by a dm mass of the rod in terms of the distance between the mass and point mass. All the forces exerted by all the dm masses of the rod are in the same direction. Therefore, the magnitude of the net force will be equal to the sum of all the forces.
Therefore, if we integrate equation (i) for limits of x from a to a+L. we will get the net force F exerted by the rod on the point mass.
Therefore,
$\int{dF}=\int\limits_{a}^{a+L}{\dfrac{Gm\left( A+B{{x}^{2}} \right)dx}{{{x}^{2}}}}$.
Here, G, m are constant. Therefore,
$F=GM\int\limits_{a}^{a+L}{\dfrac{\left( A+B{{x}^{2}} \right)dx}{{{x}^{2}}}}$
$\Rightarrow F=GM\int\limits_{a}^{a+L}{\dfrac{Adx+B{{x}^{2}}dx}{{{x}^{2}}}}$
$\Rightarrow F=GM\left[ \int\limits_{a}^{a+L}{\dfrac{Adx}{{{x}^{2}}}}+\int\limits_{a}^{a+L}{\dfrac{B{{x}^{2}}dx}{{{x}^{2}}}} \right]$
$\Rightarrow F=GM\left[ \int\limits_{a}^{a+L}{\dfrac{Adx}{{{x}^{2}}}}+\int\limits_{a}^{a+L}{Bdx} \right]$
Here, A and B are constant. Therefore, we get
$\Rightarrow F=GM\left[ -A\left. \dfrac{1}{x} \right|_{a}^{a+L}+B\left. x \right|_{a}^{a+L} \right]$
$\Rightarrow F=GM\left[ -A\left( \dfrac{1}{a+L}-\dfrac{1}{a} \right)+B\left( a+L-a \right) \right]$
$\Rightarrow F=GM\left[ A\left( -\dfrac{1}{a+L}+\dfrac{1}{a} \right)+B\left( L \right) \right]$
$\Rightarrow F=GM\left[ A\left( \dfrac{1}{a}-\dfrac{1}{a+L} \right)+B\left( L \right) \right]$
Hence, the correct option is B.

Note: Note that we could integrate the force dF only because all the forces exerted by all the dm masses of the rod were in the same direction and hence the magnitude of resultant of all the force will be the sum of the magnitudes of all the forces.
The meaning of integration is taking the sum of all the small elements to make the whole element.