Question

A stone is thrown horizontally under gravity with a speed of $10m/\sec $. Find the radius of curvature of its trajectory at the end of $3\sec $ after motion began.
(A) $10\sqrt {10} m$
(B) $100\sqrt {10} m$
(C) $\sqrt {10} m$
(D) $100m$

Answer 1

Hint: When an object follows a curved path, where its velocity is tangential to the shape of the curve formed. The radius of curvature for such a motion is given by the square of the tangential velocity of the object divided by the component of its acceleration, which is normal to this velocity.

Complete step by step answer:
Suppose that a body moves in an arbitrary curved path, the motion is caused by a velocity which is always tangential to the curve, and acceleration does not act along the same line as the velocity, in other words, it acts at an angle to the velocity. In case of a circle, this angle between acceleration and velocity is $90^\circ $. Thus, the radius of curvature formed by that instantaneous circle in a curve is given by-
$r = \dfrac{{{v_t}^2}}{{{a_N}}}$
Here,${v_t}$ is the tangential velocity.
${a_N}$ is that component of acceleration, which is perpendicular to the tangential velocity at a given instant.
And $r$ is the radius of curvature.


In the question, it is given that the ball is thrown with a horizontal velocity under the action of gravity. It follows a parabolic path due to the projectile motion.
To determine the velocity $\left( {{v_t}} \right)$at time $t = 3\sec $, we use the first equation of motion.
$\vec V = \vec U + \vec at$
Here, in the vertical direction,
The final velocity,$\vec V = {\vec v_y}\hat j$
The initial velocity, $\vec U = 0$ (it has no initial vertical velocity as the stone is thrown horizontally)
The acceleration is equal to the acceleration due to gravity,
$\vec a = - \vec g\hat j$
We have,
${\vec v_y} = 0 + ( - 10) \times 3$
$ \Rightarrow {\vec v_y} = - 30\hat j$(since it moves downwards, it has a negative sign.)
The horizontal velocity of the stone remains constant, therefore ${\vec v_x} = 10\hat i$.
The tangential velocity is given by-
${\vec v_t} = {\vec v_x}\hat i + {\vec v_y}\hat j$
$ \Rightarrow {\vec v_t} = 10\hat i - 30\hat j$
Magnitude,
\[\left| {{{\vec v}_t}} \right| = \sqrt {{{10}^2} + {{30}^2}} = \sqrt {1000} \]
$ \Rightarrow {v_t} = 10\sqrt {10} $
Now for the acceleration, the only force acting here is the gravitational force which is in the vertical direction. Therefore, to make it perpendicular to ${\vec v_t}$, we shift it by an angle $\theta $.
Such that, ${a_N} = g\cos \theta $
Since the angles ${v_x},{v_y}$ and ${v_t},{a_N}$ are both equal to $90^\circ $. Therefore the angle between ${v_x},{v_t}$ and ${v_y},{a_N}$ should also be equal to $\theta $.
Therefore,

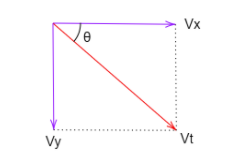
$\cos \theta = \dfrac{{{v_x}}}{{{v_t}}} = \dfrac{{10}}{{10\sqrt {10} }}$
$ \Rightarrow \cos \theta = \dfrac{1}{{\sqrt {10} }}$
The value of normal acceleration,
Taking $g = 10m/{s^2}$
${a_N} = 10 \times \dfrac{1}{{\sqrt {10} }}$
$ \Rightarrow {a_N} = \sqrt {10} $
The radius of curvature is given by,
$r = \dfrac{{{v_t}^2}}{{{a_N}}}$
$ \Rightarrow r = \dfrac{{{{(10\sqrt {10} )}^2}}}{{\sqrt {10} }} = \dfrac{{1000}}{{\sqrt {10} }}$
$ \Rightarrow r = 100\sqrt {10} $

Thus option (B) is correct.

Note: The radius of curvature is defined for circles, but curves (or the curved path traced by a particle’s motion) that do not follow the equation of a circle can also have an instantaneous radius and center of curvature. This is done by using the components of that motion, which can create a circular path