Question

A stone is dropped from the top of a building. When it crosses a point 5m below the top, another stone starts to fall from a point 25m below the top, both stones reach the bottom of the building simultaneously. The height of the building is: [Take g = 10 m/s\[^2\]]
A. 45 m
B. 35 m
C. 25 m
D. 50 m

Answer 1

Hint: Gravity is a fundamental interaction between two objects having a certain mass. It is a form of mutual attraction force between the interacting objects. The force of this mutual attraction depends on the size of the objects and the square of the distance separating them. So far, as known in Physics, Gravitational pull is the weakest known force existing in nature.

Complete step by step solution:

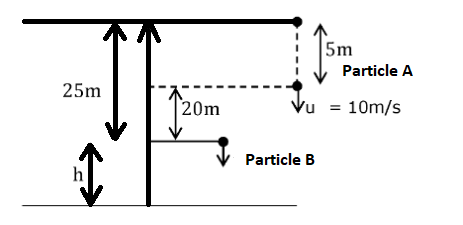
Image: Figure to explain the question

The velocity of the particle (A) at 5m below top
\[{u_1} = \sqrt {2gh} \\ \Rightarrow {u_1} = \sqrt {(2 \times 10 \times 5)} \\ \Rightarrow {u_1} = 10\,m{s^{ - 1}} \\ \]
The second law of motion is denoted by:
\[S = ut + \left( {\dfrac{1}{2}} \right)a{t^2}\]
where, S = Distance Travelled, u = Initial Velocity, t = time taken and a = acceleration.

For a particle (A), using \[{2^{nd}}\] the equation of motion, we get:
\[20 + h = 10t + \left( {\dfrac{1}{2}} \right)g{t^2} - - - - (1)\]
For a particle (B), using \[{2^{nd}}\] the equation of motion
\[h = \left( {\dfrac{1}{2}} \right)g{t^2}\]
Put equation (2) in equation (1), and we get,
\[20 + \left( {\dfrac{1}{2}} \right)g{t^2} = 10t + \left( {\dfrac{1}{2}} \right)g{t^2} \\ \Rightarrow t = 2\,\sec \\ \]

Putting the time value in equation (2), we get:
\[h = \left( {\dfrac{1}{2}} \right)g{t^2} \\ \Rightarrow h = \left( {\dfrac{1}{2}} \right) \times 10 \times {2^2} \\ \therefore h = 20m \]
Hence, the total height of the building is \[\;25 + 20 = 45m\].

Therefore, the correct answer is option A.

Note: The most fundamental principles of an object's motion are described by the equations of motion used in kinematics. In 1D, 2D, and 3D, these equations control how an object moves. Expressions like the position, velocity, or acceleration of an object at different times can be simply calculated using them.