Question

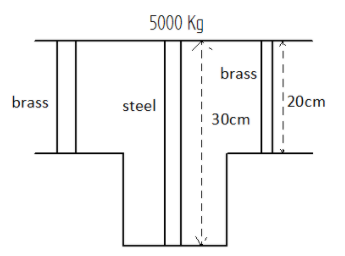
A steel rod of cross-sectional area \[16c{m^2}\] and two brass rods each of cross-sectional area \[10c{m^2}\] together support a load of \[500kg\] as shown in figure. Find the stress in the brass and steel rod (in\[kg/c{m^2}\]). Take $Y$ for steel \[ = {\text{ }}2.0 \times {10^6}kg/c{m^2}\] and for brass \[ = {\text{ }}1.0 \times {\text{ }}{10^6}kg/c{m^2}\].

A) $121,161$
B) $161,120$
C) $120,140$
D) $141,120$

Answer 1

Hint: Here we have to find the stress in the steel and the brass rod by using the data mentioned in the question. Stress is defined as a quantity that describes the magnitude of the forces that cause the deformation.

Complete step by step solution:
In question they have given the cross sectional area of a steel rod is \[{A_s} = 16c{m^2}\] and the cross sectional area of a brass rod is \[{A_B} = 10c{m^2}\]they have also given the support load that is \[W = 500kg\]
Since \[\;\Delta l\;\] will be same for both steel and brass hence the equation becomes
$\dfrac{F}{A} = Y\dfrac{{\Delta l}}{l}$
Now ${F_S} + 2{F_B} = 5000.....(1)$
Now we know the formulae to calculate stress that is
$stress(s) = \dfrac{F}{A}$
Here the given metal is steel and brass so the above can be written as
${S_s} = \dfrac{{{F_s}}}{{{A_s}}}$ , ${S_B} = \dfrac{{{F_B}}}{{{A_B}}}$
Now we want force then the above equation can be written as
${F_s} = {S_s}{A_s}$, ${F_B} = {S_B}{A_B}$
Now the stress can be written as young’s modulus $ \times $change in length to the original length so
$\Rightarrow$ ${S_s} = {Y_s}\dfrac{{\Delta {l_s}}}{{{l_s}}}$, ${S_B} = {Y_B}\dfrac{{\Delta {l_B}}}{{{l_B}}}$
Then ${S_s} \propto \dfrac{{{Y_s}}}{{{l_s}}}$ , and for brass ${S_B} \propto \dfrac{{{Y_B}}}{{{l_B}}}$
Now divide stress of steel with stress of brass so the equation become
$\Rightarrow$ $\dfrac{{{S_s}}}{{{S_B}}} = \dfrac{{{Y_s}{l_B}}}{{{Y_B}{l_s}}}$
After substituting values we get
$\Rightarrow$ $\dfrac{{{S_s}}}{{{S_B}}} = 2 \times \dfrac{2}{3}$
After calculating we get
$\Rightarrow$ $\dfrac{{{S_s}}}{{{S_B}}} = \dfrac{4}{3}$
Now we want stress of steel and the stress of brass hence the equation becomes
$\Rightarrow$ ${S_s} = \dfrac{4}{3}{S_B}$ and ${S_B} = \dfrac{3}{4}{S_s}$
In equation 1 we can write ${F_s} = {S_s}{A_s}$ and ${F_B} = {S_B}{A_B}$ so the equation becomes
$\Rightarrow$ ${S_s}{A_s} + 2{S_B}{A_B} = 5000$
Now substitute the value of stress in brass that is ${S_B} = \dfrac{3}{4}{S_s}$then
$\Rightarrow$ ${S_s}{A_s} + 2\left( {\dfrac{3}{4}{S_s}} \right){A_B} = 5000$
After simplifying the equation becomes
$\Rightarrow$ ${S_s}{A_s} + \dfrac{3}{2}{S_s}{A_B} = 5000$
Now take ${S_s}$ common so the equation will be
$\Rightarrow$ ${S_s}\left( {{A_s} + \dfrac{3}{2}{A_B}} \right) = 5000$
Now substitute the values hence we get
$\Rightarrow$ ${S_s}\left( {16 + \dfrac{3}{2} \times 10} \right) = 5000$
Now after calculating the above equation we get
$\Rightarrow$ ${S_s}\left( {31} \right) = 5000$
Therefore ${S_s} = \dfrac{{5000}}{{31}} \cong 161Kg/c{m^2}$
Now substitute the value of ${S_s}$ in the ${S_B} = \dfrac{3}{4}{S_s}$
$\Rightarrow$ \[\;{S_B} = \dfrac{3}{4} \times 161\]
After calculating we get the value of ${S_B}$, ${S_B} \cong 121Kg/c{m^2}$.

Note: Stress is generally stated as force per unit area. When forces pull on a material and cause its elongation, like the stretching of an elastic band, we call such stress a tensile stress.