Question

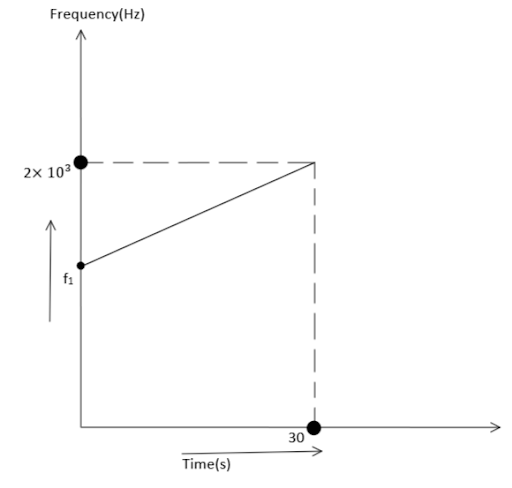
A source of sound of frequency ${f_1}$ is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency $f(Hz)$ is plotted against time $t(\sec )$ . The speed of sound in air is $300\,m/s$ . Find ${f_1}$ $\left( {g = 10m/{s^2}} \right)$ .

A. $0.5 \times {10^3}\,Hz$
B. $1 \times {10^3}\,Hz$
C. $0.25 \times {10^3}\,Hz$
D. $0.2 \times {10^3}\,Hz$

Answer 1

Hint: In such a case, the solution to a problem is trickier that’s why we have to use a different approach to solve the question. This problem is based on sound waves, we know that the frequency of a wave varies with different parameters hence, we will try to solve this problem by calculating the slope of the graph.

Formula used:
The expression of apparent frequency is,
$f = {f_1}\left( {\dfrac{{v + {v_0}}}{v}} \right) = {f_1} + \dfrac{{{v_0}}}{v}{f_1}$
Where, $f_1$ is the source frequency, $v_0$ is the speed of the observer and $v$ is the speed of sound in air.

Complete step by step solution:
The speed of sound in air is $v = 300m/s$....(given)
The observer frequency $f = 2 \times {10^3}Hz$ is taken from the graph given.
Now, we know that Apparent frequency of observer will be:
$f = {f_1}\left( {\dfrac{{v + {v_0}}}{v}} \right) = {f_1} + \dfrac{{{v_0}}}{v}{f_1}$… (1)
Using 1st Equation of motion, we have ${v_0} = gt$
where, $g = 10m/{s^2}$ = Acceleration due to gravity (given)

From (1), we get
$f - {f_1} = \left( {\dfrac{{{f_1}g}}{v}} \right)t$
where, $\dfrac{{{f_1}g}}{v}$ = Slope of the given graph
The above expression can also be written as:
$\dfrac{{f - {f_1}}}{t} = \dfrac{{{f_1}g}}{v}$ … (2)
Substituting all the value given in the question in eq. (2) at time $t = 30\,s$, we get
$\dfrac{{2 \times {{10}^3} - {f_1}}}{{30}} = \dfrac{{{f_1} \times 10}}{{300}} \\ $
$ \therefore {f_1} = 1 \times {10^3}Hz$
Thus, the frequency of a source of sound is $1 \times {10^3}Hz$.

Hence, the correct option is B.

Note: The Doppler effect is a significant phenomena in many scientific areas, including planetary science. The Doppler effect, often known as the Doppler shift, explains variations in the frequency of any sound or light wave produced by a moving source in relation to an observer.