Question

A solid sphere of mass 2 $kg$ radius 0.5$m$ is rolling with an initial speed of 1 $m{s^{ - 1}}$ goes up an inclined plane which makes an angle of ${30^ \circ }$ with the horizontal plane, without slipping. How long will the sphere take to return to the starting point A?

1. $0.80$ sec
2. $0.60$ sec
3. $0.52$ sec
4. $0.57$ sec

Answer 1

Hint: In this question, we are given a solid sphere which is rolling with an initial speed 1 $m{s^{ - 1}}$ goes up an inclined plane and make ${30^ \circ }$ angle with the horizontal plane. We have to find the total time taken by the sphere to go up and return. First step is to equate the force to find the acceleration. Then, apply the formula \[Time{\text{ }}taken = \dfrac{{velocity}}{{acceleration}}\] to calculate the time. Also, while calculating the time double the velocity as it is same in time of ascent and decent

Formula used:
Moment of inertia (solid sphere) $I = \dfrac{2}{5}m{r^2}$
Formula of time in terms of velocity and acceleration –
\[Time{\text{ }}taken = \dfrac{{velocity}}{{acceleration}}\]

Complete answer:
Given that,
Mass of the solid sphere, $m = 2kg$
Radius of the sphere, $r = 0.5m$
Initial speed of the sphere, $u = 1m{s^{ - 1}}$
Angle of inclination $ = {30^ \circ }$

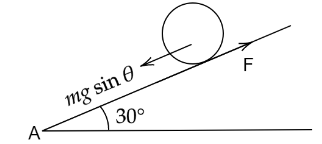
Now, the force of the solid sphere going upward is $F = \dfrac{{mg\sin \theta }}{{1 + \dfrac{I}{{m{r^2}}}}}$
Moment of inertia of the solid sphere is $I = \dfrac{2}{5}m{r^2}$
It implies that,
$ma = \dfrac{{mg\sin \theta }}{{1 + \dfrac{{\left( {\dfrac{2}{5}m{r^2}} \right)}}{{m{r^2}}}}}$
$a = \dfrac{{g\sin {{30}^ \circ }}}{{\left( {1 + \dfrac{2}{5}} \right)}}$

Here, acceleration of gravity $g = 9.8m{s^{ - 2}}$
$a = \dfrac{5}{7} \times \dfrac{{9.8}}{2}$
$a = 3.5m{s^2}$

As we know that,
\[Time{\text{ }}taken = \dfrac{{velocity}}{{acceleration}}\]

Due to symmetry time of ascent and decent will be same. Therefore, initial velocity will be double,
\[t = \dfrac{{2u}}{a}\]
\[t = \dfrac{{2\left( 1 \right)}}{{\left( {3.5} \right)}}\]
$t = 0.57$ sec

Hence, Option (4) is the correct answer i.e., $0.57$ sec.

Note: The key concept involved in solving this problem is the good knowledge of moment of inertia. Students must remember that in physics, a moment of inertia is a quantitative measure of a body's rotational inertia—that is, the resistance that the body exhibits to having its speed of rotation about an axis altered by the application of a torque (turning force). The axis can be internal or external, and it can be fixed or not.