Question

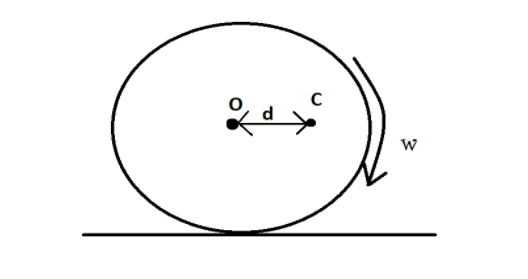
A solid sphere is rolling on a rough surface, whose centre of mass is at $C$ at a certain instant. At that instant it has angular velocity $\omega $ and its radius is $R$. Find angular acceleration at that instant. Mass of the sphere is $m$.


(A) $\dfrac{5}{2}\dfrac{{gd}}{{{R^2}}}$
(B) $\dfrac{5}{7}\dfrac{{gd}}{{{R^2}}}$
(C) $\dfrac{5}{2}\dfrac{{d(g + {\omega ^2}R)}}{{{R^2}}}$
(D) $\dfrac{5}{7}\dfrac{{d(g + {\omega ^2}R)}}{{{R^2}}}$

Answer 1

Hint:As we can see in the figure, the centre of mass of the sphere is not at the centre of the body due to which there is some torque applied on the sphere. Surface is rough then due to force of friction some force is applied in the opposite direction which also applies some torque. Due to these torques, there is some angular acceleration of the sphere.

Complete step by step solution
Centre of mass of the sphere is at distance of $d$ from the centre of the body. Means there is some torque on sphere due to its gravitational force which is given by
${\tau _1} = F \times d = mgd$, here $g$ is gravity due to earth.
The surface is rough means, there is force of friction between sphere in backward or left direction and it also apply some torque on sphere is given by
${\tau _1} = F \times R = m{\omega ^2}Rd$, here $R$ is radius of surface.
We know that the moment of inertia of a given sphere is $I = \dfrac{7}{5}m{R^2}$.
We know that net torque is equal to the product of moment of inertia and angular acceleration.
Let angular acceleration of the sphere is $\alpha $.
Then, ${\tau _1} + {\tau _2} = I\alpha $
$\alpha = \dfrac{{{\tau _1} + {\tau _2}}}{I} = \dfrac{{mgd + m{\omega ^2}Rd}}{{\dfrac{7}{5}m{R^2}}} = \dfrac{5}{7}\dfrac{{md(g + {\omega ^2}R)}}{{m{R^2}}}$
$\alpha = \dfrac{5}{7}\dfrac{{d(g + {\omega ^2}R)}}{{{R^2}}}$

Hence the correct answer is option D.

Note: Surface is rough means sphere is in pure rolling motion. Here we have given solid sphere and we know that the moment of inertia for a solid sphere is $I = \dfrac{7}{5}m{R^2}$, if sphere is hollow then answer may be different because moment of inertia changes.