Question

A solid current-carrying conductor of radius R is having current per unit area ( $J$ ) as $J = \dfrac{{\alpha r}}{R}$ where $\alpha$ is a constant and $r$ is the distance from the axis. Find the magnetic field at a distance $x$ from the axis of the wire.
Assume $x > R$.
A) $\dfrac{{{\mu _0}\alpha {x^2}}}{{3R}}$
B) $\dfrac{{{\mu _0}\alpha {x^2}}}{{2R}}$
C) $\dfrac{{{\mu _0}\alpha {R^2}}}{x}$
D) $Zero$

Answer 1

Hint: We apply Amperes’ Circuital Law. The magnetic field is directly proportional to the current, which acts as its source. Like Gauss’ Law, Amperes’ Circuital Law is very useful when calculating magnetic fields of current distributions with high symmetry.

Complete step by step solution:
The Amperes’ Circuital Law relates current to the magnetic field created by it.
This law states that the integral of magnetic field density $B$ along an imaginary closed path is equal to the product of current enclosed by the path and permeability of the medium.
$\oint {\vec B.d\vec l = {\mu _0}} I$
where, $\oint {\vec B.d\vec l}$ is line integral of B around a closed path
${\mu _0} = 4\pi \times {10^{ - 15}}N{A^{ - 2}}$ is the permeability of free space
$I$ is current
The magnetic field lines encircle the current-carrying wire, and the magnetic field lines lie in a plane perpendicular to the wire.
A closed- loop called the Amperian loop is designated to find a magnetic field using this law. We assume the loop consists of small elemental rings of thickness dr.
The length of the small element mentioned as $dl$ of the elemental rings taken here is its circumference, i.e., $2\pi x.dx$
Take an elemental ring of thickness $dx$ at a distance of $x$ from the center.

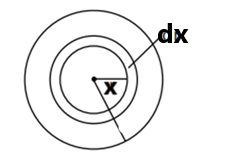
By Amperes’ Circuital Law,
$\oint {B.dl = {\mu _0}} I$
$\therefore B \times 2\pi x = {\mu _0}I$……..$(1)$
Now,
$\Rightarrow dI = J \times area$
$\Rightarrow \dfrac{{\alpha x}}{R} \times (2\pi x)dx$
$\Rightarrow \dfrac{{2\pi \alpha }}{R}{x^2}dx$
Integrating to find the total current from the center to a distance x:
$\Rightarrow I = \int\limits_0^x {\dfrac{{2\pi \alpha }}{R}} {x^2}.dx$
$\Rightarrow I = \dfrac{{2\pi \alpha }}{R}[\dfrac{{{x^3}}}{3}]_0^x{\text{ }}$
The formula of basic integration used is, ${\text{ }}\int {{x^n}} .dx = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C$
$\Rightarrow I = \dfrac{{2\pi \alpha }}{R}.\dfrac{{{x^3}}}{3}$
Applying the current calculated in the equation $(1)$, we get
$\Rightarrow B \times 2\pi x = {\mu _0}I$
$\Rightarrow B \times 2\pi x = {\mu _0}\dfrac{{2\pi \alpha }}{R}.\dfrac{{{x^3}}}{3}$
$\Rightarrow B = \dfrac{{{\mu _0}\alpha {x^2}}}{{3R}}$

The correct answer is [A], $\dfrac{{{\mu _0}\alpha {x^2}}}{{3R}}$.

Note: Whenever a body with the non-uniform current is mentioned, its total current is calculated by integration. Only the current inside the closed path is taken into consideration because only that current contributes to the magnetic field.