Question

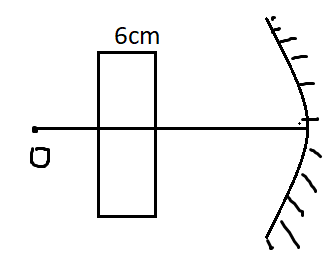
A slab of glass, of thickness 6 cm and refractive index \[\mu = 1.5\] is placed in front of a concave mirror as shown in the figure. If the radius of curvature of the mirror is 40 cm and the reflected image coincides with the object, then the distance of the object from the mirror is.

(A) 30cm
(B) 22cm
(C) 42cm
(D) 38cm

Answer 1

Hint It is given that the given mirror is concave. Hence the image formed will be upside down and its magnification depends upon its position placed. Use the shift produced by a glass slab of different refractive index formula to find the shift and add the value with radius of curvature to find the object distance.

Complete Step By Step Solution
Concave mirrors are examples of converging mirrors. The image produced due to reflection will naturally be inverted and real in nature. Now , when a glss slab of selective refractive index is placed in front of the object at a distance, the image produced will not be clear but rather will seem to be deflected from its original form.
It is also said that the reflected image will coincide with the object. In a concave mirror , this is only possible when the object is placed at the radius of curvature of the mirror.
Now radius of curvature of the mirror is given as,
\[R = 40cm\], thus it’s focal length is equal to\[f = 20cm\].
Now in the final image, the shift from the original object to the final image produced by the slab of refractive index is calculated using,
\[s = t[1 - \dfrac{1}{\mu }]\], where s is the shift produced due to the slab, t is the thickness of the glass slab and \[\mu \]is the refractive index of the given glass slab.
\[ \Rightarrow s = 6 \times [1 - \dfrac{1}{{1.5}}]\]
\[ \Rightarrow s = 6 \times [\dfrac{1}{3}]\]
\[ \Rightarrow s = 2cm\]
Now, we know that there is a 2cm shift in the object due to the presence of the glass slab. Therefore the initial position of object will be
\[R + s = 40cm + 2cm = 42cm\]

Therefore, Option (c) is the right answer.

Note Refractive index of any material is defined as the number that determines how fast the light travels through another medium from one medium. It is mathematically given as the ratio between speed of light and the velocity of the light in the second medium.