Question

A semicircle loop PQ of radius $R$ is moved with velocity $v$ in transverse magnetic field as shown in fig. The value of induced emf at the end of the loop is
  
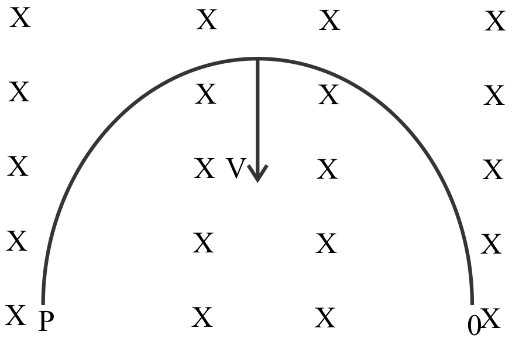
A. $Bv\pi R$ end P at high potential
B. $2BRv$end P at high potential
C. $2BRv$end Q at high potential
D. $\dfrac{{B\pi {R^2}v}}{2}$ end P at high potential

Answer 1

Hint: First put the above values in the formula for induced emf in a conductor moving with a given velocity. One important thing to consider is that the emf induced only depends upon the ends of the conductor and not the shape. Then using Fleming’s right hand rule, we can determine which end will have high potential.

Formula used:
$\varepsilon = Bvl$ where $\varepsilon $is the emf induced in the conductor of length $l$ when it moves in a magnetic field $B$ with velocity $v$.
$\varepsilon = - \dfrac{{d\Phi }}{{dt}}$ where $\Phi $ is the magnetic flux linked with the conductor.

Complete step by step solution
When a conductor of length $l$ is moving with a constant velocity $v$ in a magnetic field $\overrightarrow B $, an emf or a potential difference is induced between the two ends of the conductor. This emf is given as,
$\varepsilon = Bvl$when the conductor moves in a direction perpendicular to the magnetic field
Taking $l = 2R$ as the induced emf only depends upon the ends of a conductor.
Therefore, $\varepsilon = 2BRv$
Another way of calculating the emf induced within the conductor is by taking the time derivative of the magnetic flux linked with the conductor, which is given as,
$\varepsilon = - \dfrac{{d\Phi }}{{dt}}$
The magnetic flux through the conductor is given as,
$\Phi = BA$$ = Bldx$
So, $\varepsilon = - 2BR\dfrac{{dx}}{{dt}}$ [As induced emf only depends upon the ends of a conductor, $l = 2R$]
$ \Rightarrow \varepsilon = - 2BRv$
Taking the absolute value we get,
$\varepsilon = 2BRv$
This is the emf induced in the semicircular loop PQ.
Now, by using Fleming’s right hand rule which states that if we stretch the right-hand thumb and two nearby fingers perpendicular to one another, and the first finger points in the direction of the magnetic field and the thumb is in the direction of motion of the conductor, then the middle finger will point in the direction of the induced current, we can show that P is at low potential and Q is at high potential.

So, the correct option is C.

Note: The direction of the induced emf, or the current, in any circuit is such as to oppose the cause that produces it. This is known as Lenz’s law.