Question

A rope ladder of length \[L\] is attached to a balloon of mass \[M\]. As the man of mass \[m\]climbs the ladder into the balloon basket, the balloon comes down by a vertical distance \[s\]. Then the increase in potential energy of man divided by the increase in potential energy of balloon is

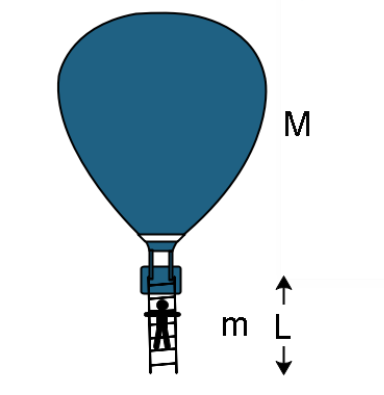
A) \[\dfrac{{L - s}}{s}\]
B) $\dfrac{L}{s}$
C) $\dfrac{s}{{L - s}}$
D) $L - s$

Answer 1

Hint: The potential energy of an object is due to its position with respect to the surface form the heart. When an object rises, its potential energy increases, and when it falls, its potential energy increases.
Formula used: In this solution, we will use the following formula:
Potential energy of an object $U = mgh$ where $m$ is the mass of the object $g$ is the gravitational acceleration and $h$ is the height

Complete step by step answer:
In the scenario given to us, the man is climbing the ladder of the balloon. When the man climbs the ladder his height increases with respect to the ground. As a result, the potential energy of the man also increases.
Since the balloon also drops by a vertical distance $s$ when the man is climbing the ladder, the net change in height of man when he has climbed the ladder will be $l - s$.
Hence the change in potential energy of the man will be
${U_m} = mg(l - s)$
This change in potential energy will be compensated by the work done by the man and the change in potential energy of the balloon, so we can write
${U_B} = W + {U_M}$
S, the work done by the man will be the product of the force acting on him $(mg)$ and the displacement of the man $(l)$.
\[{U_B} = mgl + mg(l - s)\]
\[ \Rightarrow {U_B} = mgs\]
Hence the ratio of the changes in potential energy will be
$\dfrac{{{U_m}}}{{{U_B}}} = \dfrac{{mg(l - s)}}{{mgs}}$
Which gives us
$\dfrac{{{U_m}}}{{{U_B}}} = \dfrac{{l - s}}{s}$

Hence the correct choice is option (A).

Note: It is easy to expect that the change in potential energy of the man will be directly equal to the change in potential energy of the balloon, however that is not the case, since the man does work on the balloon when he climbs it which has to be taken into account. Additionally, we must be careful while calculating the change in height of the man as $(l - s)$ and not $(s)$.