Question

A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is
A. $\dfrac{{W\left( {d - x} \right)}}{x}$
B. $\dfrac{{W\left( {d - x} \right)}}{d}$
C. $\dfrac{{Wx}}{d}$
D. $\dfrac{{Wd}}{x}$

Answer 1

Hint In the question, the weight of the rod is supported by two parallel edges, it is in a horizontal position. Imaginate the situation by the given parameters and equation the forces of the positions, then we get the normal reaction on A.

Complete step by step answer
The situation is given below in the diagrammatic representation.
 
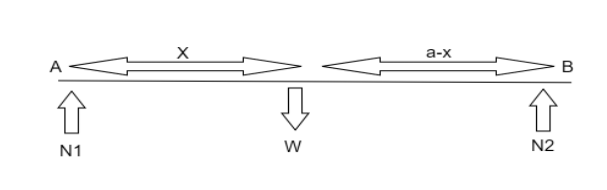
Where,
${N_1}$ be the Normal reaction on A,${N_2}$be the Normal reaction on B and $W$be the weight of the rod.
Equating the forces and taking the vertical equilibrium by the normal reaction, we get
${N_1} + {N_2} = W........\left( 1 \right)$
In the diagram, Torque balance about centre of mass of the rod, so we get the expression as
$Nx = {N_2}\left( {d - x} \right)........\left( 2 \right)$
Convert the equation 1 in terms of the normal reaction on B, we get
${N_2} = W - {N_1}$
Substitute the value of ${N_2}$in the equation 2, we get
\[Nx = \left( {W - {N_1}} \right)\left( {d - x} \right)\]
Simplify the above equation, we get
\[Nx = \left( {Wd - Wx - {N_1}d + Nx} \right)\]
Taking the common terms and simplify the equation, we get
$Nd = W\left( {d - x} \right)$
Convert the equation in terms in terms of the normal reaction on A, we get
${N_1} = \dfrac{{W\left( {d - x} \right)}}{d}$
Therefore, the normal reaction on A is $\dfrac{{W\left( {d - x} \right)}}{d}$.

Hence from the above options, option B is correct.

Note In the question, we know that the two edges are in the same direction that is in the vertical position. So, vertical position, we will take it as positive. If it is in a horizontal position, we will take it as a negative sign. By equating the equations, the normal reaction on A has been calculated.