Question

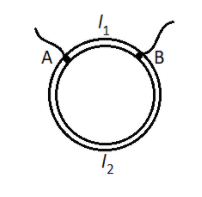
A ring is made of a wire having a resistance ${R_0} = 12\Omega $. Find the points A and B as shown in figure, at which a current carrying conductor should be connected, so that the resistance $R$ of the sub circuit between these points is equal to $\dfrac{8}{3}\Omega $



A) $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{5}{8}$
B) $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{1}{3}$
C) $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{3}{8}$
D) $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{1}{2}$

Answer 1

Hint: In order to find the ration between the in-between lengths of the circuit, remember the resistance of the conductor is proportional to the length of that conductor. When we take resistance between two points in a wire ring we consider the ring as two different sub circuits which are in parallel connection.

Complete step by step solution:Let’s define all the data given in the question.
The resistance of the wire used to make the ring, ${R_0} = 12\Omega $
Resistance of the sub circuit between the points A and B, $R = \dfrac{8}{3}\Omega $
We are asked to find out the ratio between the two lengths that formed in between the two points A and B as shown in the figure.
We know the resistance of a wire, $R = \dfrac{{\rho l}}{A}$
Where, $\rho $ is the resistivity of the wire
$l$ is the length of the wire
$A$ is the cross-sectional area of the wire
In this case the same wire is used for both lengths, so the resistivity and the cross sectional area of the wire will be the same for both lengths.
So, the resistance will be proportional to the length of the wire.
That is, $R \propto l$
When we consider the whole ring as two sub circuits between the two points A and B, we can see that these two circuits are in a parallel connection.
Let ${R_1}$ be the resistance of length ${l_1}$
And ${R_2}$ be the resistance of length ${l_2}$
$\therefore {R_1} + {R_2} = {R_0} = 12\Omega $ …………………………………….. (1)
In a parallel connection, we know,
\[ \Rightarrow \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} = \dfrac{3}{8}\]
\[ \Rightarrow \dfrac{{{R_1} + {R_2}}}{{{R_1}{R_2}}} = \dfrac{3}{8}\]
Applying the value from equation (1), we get,
\[ \Rightarrow \dfrac{{12}}{{{R_1}{R_2}}} = \dfrac{3}{8}\]
\[ \Rightarrow \dfrac{4}{{{R_1}{R_2}}} = \dfrac{1}{8}\]
\[ \Rightarrow {R_1}{R_2} = 32\]
We know, \[{\left( {a + b} \right)^2} = {a^2} + {b^2} = 2ab\]
\[ \Rightarrow {\left( {{R_1} + {R_2}} \right)^2} = {R_1}^2 + {R_2}^2 + 2{R_1}{R_2}\]
\[ \Rightarrow {12^2} = {R_1}^2 + {R_2}^2 + 2 \times 32\]
\[ \Rightarrow 144 - 64 = {R_1}^2 + {R_2}^2\]
\[ \therefore 80 = {R_1}^2 + {R_2}^2\]
Solving this equation we get two values for ${R_1}$ and ${R_2}$, $4$ and $8$
We choose ${R_1} = 4$ and ${R_2} = 8$ according to the options given, so,
$\therefore$ $\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{l_1}}}{{{l_2}}} = \dfrac{4}{8} = \dfrac{1}{2}$

The correct option is (D), $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{1}{2}$.

Note: The term resistance is a measure of how difficult it is to transmit current through a wire. The term resistivity is a characteristic of the material used in a wire or any electrical component, whereas the resistance is a characteristic of the electrical component or wire. Resistance of a wire depends on the resistivity of the material used.