Question

A radioactive nuclide X decays into nuclei Y and Z by simultaneous disintegration as shown. Effective decay constant for the disintegration is

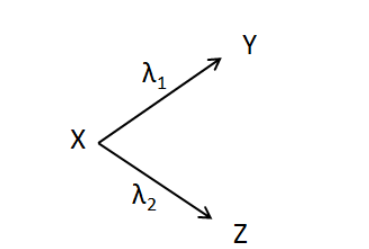
(A) ${\lambda _1} + {\lambda _2}$
(B) $\dfrac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$
(C) $\dfrac{{{\lambda _1} + {\lambda _2}}}{2}$
(D) $\dfrac{{2{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$

Answer 1

Hint: To solve this question, we need to use the general equation for the rate of nuclear disintegration. We have to apply the equation separately for the two decays of the given nucleus, and combine them to get the effective decay constant.

Complete step-by-step solution:
We know that the rate of the radioactive decay of a nucleus is proportional to the number of nuclei. And the constant of this proportionality is the decay constant. So the expression for the rate of the radioactive decay of a nucleus is written as
$ - \dfrac{{dN}}{{dt}} = \lambda N$
Now, according to the given nuclide X is being decayed into the two daughter nuclei Y and Z. And the decay constants for these two decays are given to be ${\lambda _1}$ and ${\lambda _2}$ respectively.
So we can separately write the equation for the rate of decay for these two decays. Writing the equation for the decay of X to Y, we get
$ - \dfrac{{d{N_X}}}{{dt}} = {\lambda _1}{N_X}$
Every decayed nucleus of X produces a nucleus Y. So we can write
$\dfrac{{d{N_Y}}}{{dt}} = {\lambda _1}{N_X}$...................(1)
Similarly for the decay of X to Z, we can write
$\dfrac{{d{N_Z}}}{{dt}} = {\lambda _2}{N_X}$.....................(2)
Adding (1) and (2) we have
$\dfrac{{d{N_Y}}}{{dt}} + \dfrac{{d{N_Z}}}{{dt}} = {\lambda _1}{N_X} + {\lambda _2}{N_X}$
$ \Rightarrow \dfrac{{d\left( {{N_Y} + {N_Z}} \right)}}{{dt}} = \left( {{\lambda _1} + {\lambda _2}} \right){N_X}$ (3)
Now, since Y and Z nuclei are produced from the nucleus X, so we can write
\[\dfrac{{d\left( {{N_Y} + {N_Z}} \right)}}{{dt}} = - \dfrac{{d{N_X}}}{{dt}}\]
Substituting this above, we get
$ - \dfrac{{d{N_X}}}{{dt}} = \left( {{\lambda _1} + {\lambda _2}} \right){N_X}$
Comparing with the general decay rate equation $ - \dfrac{{dN}}{{dt}} = \lambda N$, we get the effective decay constant for the given disintegration as
$\lambda = {\lambda _1} + {\lambda _2}$
Thus, the effective decay constant for the disintegration of the nucleus X into the nuclei Y and Z is equal to ${\lambda _1} + {\lambda _2}$.

Hence, the correct answer is option A.

Note: The phenomenon of radioactivity is used on a large scale to generate electric power. Also, it is used in the diagnosis and treatment of diseases in the field of nuclear medicine. The diseases which can be treated by radioactivity are thyroid, cancers etc.