Question

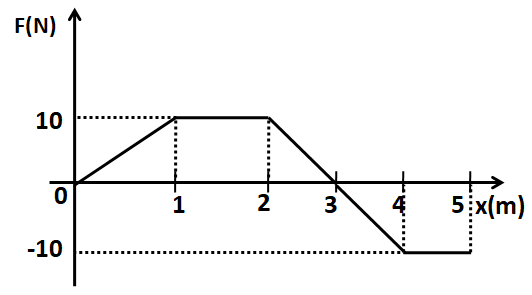
A position dependent force $F$ is acting on a particle and its force-position curve is shown in the figure. Work done on the particle, when its displacement is from $0$ to $5m$ is?

(A) \[35{\text{J}}\]
(B) $25{\text{J}}$
(C) \[15{\text{J}}\]
(D) $5{\text{J}}$

Answer 1

Hint: The work done on a particle by a force is equal to the area under the force-position curve for the particle. So we need to find the area under the curve in the given range of position of the particle.

Complete step-by-step solution:
We know that the work done by a force on a particle in displacing a particle is equal to the product of the force and the displacement. So it can be given by
$W = Fx$
But if the force is variable, then we consider the small work done by the force in displacing the particle through a small displacement $dx$ as below
$dW = Fdx$
For total work done, we integrate both sides to get
$\int_0^W {dW} = \int_{{x_1}}^{{x_2}} {Fdx} $
$ \Rightarrow W = \int_{{x_1}}^{{x_2}} {Fdx} $
So the work done is equal to the integration of the force with respect to the displacement. We know that the integration is geometrically interpreted as the area. So the work done is equal to the area under the force position curve given in the question. Now, we label the given curve as shown in the below figure

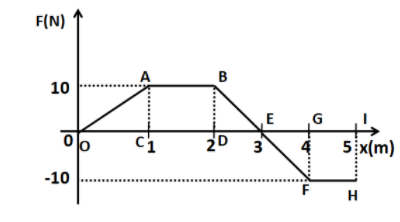
We can see that the curve consists of two trapeziums, OABE and EFHI. So the work done is given by
$W = \dfrac{{AC}}{2}\left( {AB + OE} \right) - \dfrac{{FG}}{2}\left( {FH + EI} \right)$
$ \Rightarrow W = \dfrac{{10}}{2}\left( {1 + 3} \right) - \dfrac{{10}}{2}\left( {1 + 2} \right)$
On solving we get
$W = 5{\text{J}}$
Thus, the work done is equal to $5{\text{J}}$.

Hence, the correct answer is option D.

Note: Make it sure to add the areas of the shapes of the curve algebraically, and not their absolute values. This is because for the curve which lies below the x-axis, the work done is negative. Also, we could make the solution easy by identifying similar shapes above and below the x-axis, so that their areas get cancelled and the area of the remaining shape would be the final answer.