Question

A point source of sound is located somewhere along the x-axis. Experiments show that the same wave front simultaneously reaches listeners at $x = - 8m$ and $x = + 2.0m\,$. And a third listener is positioned along the positive y-axis. What is her y-coordinate (in m) if the same wave front reaches her at the same instant as it does the first two listeners on the x-axis?

Answer 1

Hint: First start with finding the position of source of sound that is reaching both the listeners whose positions are already given in the question. Then find the distance between the source of sound and the third listener. Then find the time and hence we finally get the position of third listener at the y-axis.

Formula used:
The formula for time and speed
$t = \dfrac{d}{s}$
where, d is the distance or here the position and s is the speed of sound which is here c.

Complete step by step solution:
We have been given position of the two listeners present at the x-axis as follows-
$x = - 8m\,and\,x = + 2.0m$
From the question we know that the sound source will reach to both the listener at the x-axis so it must be between the two. Let that point source of sound be present at $x={{x}_{1}}$ on the $x-axis$.


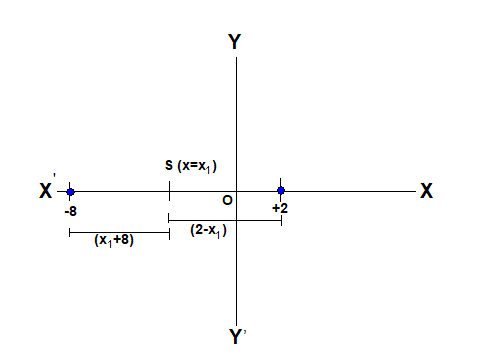
Let the speed of sound be c. Sound reaches to the two listeners in time t. We know the formula for time and speed,
$t = \dfrac{d}{s}$
Now putting all the values we get,
$t = \dfrac{{2 - x}}{c} = \dfrac{{x - 8}}{c}$
By solving we get;
$x = - 3$
So the source of sound is present at the x-axis at $x = - 3m$.

Let the position of the third listener at the $y-axis$ be $y={{y}_{1}}$ and the distance between source of the sounds and listener be $d$.

Now from the above figure we get the right angle triangle,
Put all the values in the below equation-
$d=\sqrt{{{({{y}_{1}})}^{2}}+{{(-3)}^{2}}}$
$\Rightarrow d=\sqrt{y_{1}^{2}+9}$
Given same wave front reaches her at the same instant as it does the first listener,
then we can write,
$t=\dfrac{d}{v}$ =$\dfrac{\sqrt{y_{1}^{2}+9}}{c}=\dfrac{{{x}_{1}}+8}{c}$
$\Rightarrow \sqrt{y_{1}^{2}+9}=(-3)+8=5$
$\Rightarrow y_{1}^{2}+9=25$
$\Rightarrow y_{1}^{2}=16$
By solving we get;
$\therefore {{y}_{1}}=4\,m$

Hence the third listener is at the y-axis at $4\,m$.

Note: Find the position of source of sound first by using the given condition in the question. Use the same formula as it is given here, not the other formula for the time. Do not miss any plus or minus sign otherwise the coordinate will get changed and you will not get the right answer so be careful while marking the position of the two listeners