Question

A point charge $q = 24{\varepsilon _0}$ Coulomb is kept above the midpoint of the edge of length $2a$ as shown in the figure. Line AB is perpendicular to the plane of the rectangle. Find the flux through the rectangle shown in the figure.

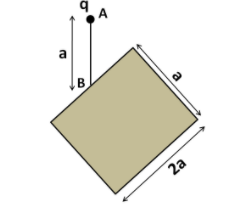
Answer 1

Hint: To solve this question, we need to use the gauss theorem. For this, we need to place the given charge in a closed volume, which has to be generated by using the rectangles given in the question. Then by using the unitary method we can find out the value of required flux through the given rectangle.

Complete step-by-step solution:
We know from the Gauss theorem that the total flux through a closed surface due to a point charge placed within it is given by
$\varphi = \dfrac{q}{{{\varepsilon _0}}}$................(1)
So we have to enclose the given point charge within a closed surface, symmetrically. We start by placing a similar rectangle adjacent to the given rectangle, so that the point charge is directly above the centre of the square thus formed, as shown in the figure below.

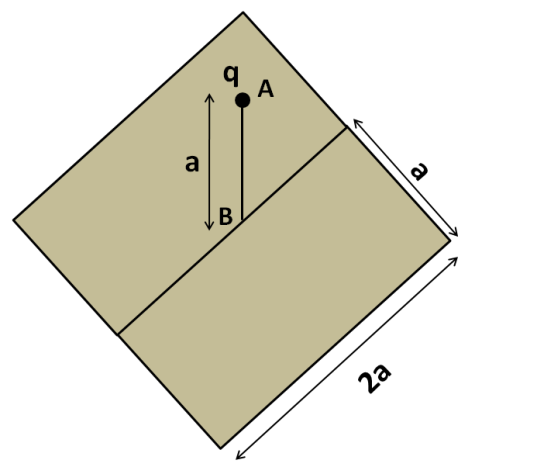
So now we have our point charge placed at above the centre of the square of side $2a$.
For generating a closed volume, we have to place five additional such squares of side $2a$ to form a cube of side $2a$. The charge will be symmetrically inside the cube. So from (1) the flux passing from this cube is
$\varphi = \dfrac{q}{{{\varepsilon _0}}}$
As the charge is symmetrically present within the cube, so the flux through each of the squares of side $2a$ is the same. As we have a total of six such squares, so the flux passing through the base square is
$\varphi ' = \dfrac{q}{{6{\varepsilon _0}}}$
Now, the base square of side $2a$ is made by placing two rectangles of dimensions $2a \times a$. As the charge is symmetrically placed with respect to their combination, as shown in the above figure, the flux passing through each of these rectangles is
$\varphi '' = \dfrac{q}{{12{\varepsilon _0}}}$
According to the question, $q = 24{\varepsilon _0}C$. Substituting this above, we finally get
$\varphi '' = 2N{m^2}/C$

Hence, the flux through the given rectangle is equal to $2N{m^2}/C$.

Note: The application of the gauss theorem does not depend on the symmetric placement of the charge within the closed surface. The charge just needs to be present within it. But for calculating the flux through a particular portion of the closed surface, we need the symmetry.