Question

A point charge of charge q and mass m is placed at rest at point X at distance r from a short electric dipole. The initial acceleration of charge ${[ a=\dfrac{k\times q\times p}{2mr^3}n ]}$, where ${[ k=\dfrac{1}{4\pi\varepsilon_0} ]}$ then n is-
A. 6.4
B. 2.6
C. 5.0
D. 8.9

Answer 1

Hint:As we know the force is mass multiplied by acceleration but in the gravitational force the acceleration is acceleration due to gravity so acceleration does not depend on the mass and in electric force the acceleration depends on the mass. As we break the component P it breaks into component Ep1 and Ep2 axial and equatorial respectively.



Formula used:
${f=m\times a}$
${f=q\times\vec{E}}$
${\left|\vec{E}\right|=\sqrt{\left|\vec{E}p_1\right|^2+\left|\vec{Ep_2}\right|^2}}$

Complete answer:
As we know force is-
${f=m\times a}$
and, ${f=q\times\vec{E}}$
where, m = mass
a = acceleration
q = given charge
E = electric field
Now to find out the net electric field from the dipole first we need to divide p in two parts which is p1 and p2 whose values are cosϴ and sinϴ respectively.
p1 = cos ϴ
p2 = sin ϴ
These are the two components of our dipole equatorial and axial, equatorial position will be at the 180˚ of the p2 which is Ep2 and along the axis of p1 will be Ep1.
Now for equatorial position our electric field will be-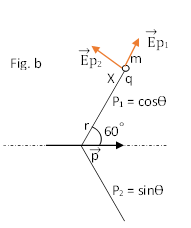
${{\vec{E}}_{(equatorial)}=\dfrac{pk}{r^3}}$
${Since,[ k=\dfrac{1}{4\pi\varepsilon_0} ]so,}$
${{\vec{E}}_{(equatorial)}=\dfrac{p}{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
${{\vec{E}}_{p_2}=\dfrac{p}{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
${{\vec{E}}_{(equatorial)}=\dfrac{p\ sin\theta}{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
As we know that the angle ϴ is 60˚ so
${Sin\ 60˚ =32 }$
${{\vec{E}}_{(equatorial)}=\dfrac{p\ }{r^3}\times\dfrac{1}{4\pi\varepsilon_0}\times\dfrac{\sqrt3}{2}}$
Now for axial position our electric field will be-
${{\vec{E}}_{(axial)}=\dfrac{2pk}{r^3}}$
${Since, [ k=\dfrac{1}{4\pi\varepsilon_0} ] so,}$
${{\vec{E}}_{(equatorial)}=\dfrac{2p}{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
${{\vec{E}}_{p_2}=\dfrac{2p}{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
${{\vec{E}}_{(equatorial)}=\dfrac{2p\ cos\theta}{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
As we know that the angle ϴ is 60˚ so
${cos\ 60˚ =12 }$
${{\vec{E}}_{(equatorial)}=\dfrac{2p\ }{r^3}\times\dfrac{1}{4\pi\varepsilon_0}\times\dfrac{1}{2}}$
${{\vec{E}}_{(equatorial)}=\dfrac{p\ }{r^3}\times\dfrac{1}{4\pi\varepsilon_0}}$
To determine magnitude of acceleration first we will determine with the help of magnitude of ${force-\left|\vec{f}\right|=m\times\left|\vec{a}\right| }$ -------(i)
${\left|\vec{f}\right|=q\times\left|\vec{E}\right|}$ -------(ii)
Equating both the equations of force (i) and (ii)
${m\times\left|\vec{a}\right|=q\times\left|\vec{E}\right| }$
${\left|\vec{a}\right|=\dfrac{q\times\left|\vec{E}\right|}{m} }$ ---------(iii)
Now magnitude of E will be,
${\left|\vec{E}\right|=\sqrt{\left|\vec{E}p_1\right|^2+\left|\vec{Ep_2}\right|^2}}$
${\left|\vec{E}\right|=\sqrt{\dfrac{p^2k^2}{r^6}+\dfrac{3}{4}\dfrac{p^2k^2}{r^6}}}$
${\left|\vec{E}\right|=\dfrac{pk}{r^3}\sqrt{1+\dfrac{3}{4}}}$
${\left|\vec{E}\right|=\dfrac{pk}{r^3}\sqrt{\dfrac{7}{4}}}$
${\left|\vec{E}\right|=\dfrac{pk}{2r^3}\sqrt7}$
Now, from equation (iii) putting value of mode E acceleration will be-
${\left|\vec{a}\right|=\dfrac{q\times p\times k}{2mr^3}\sqrt7 }$ --------(iv)
Now as given in question
${a=\dfrac{k\times q\times p}{2mr^3}n }$ -------(v)
Now equating both the equation (v) and(iv)
${\dfrac{k\times q\times p}{2mr^3}n=\dfrac{q\times p\times k}{2mr^3}\sqrt7}$
${n=\sqrt7}$
${n=2.645}$
Thus, the value of n is 2.6 and correct option is (B)





Note:Axial line is the line that passes through both the poles of the dipole the positive and the negative poles so basically it is through its axis, so it is called axial component and equatorial component is the component that is perpendicular to axial component.