
A pilot in a plane wants to go $500\;km$ towards the north. To reach straight to his desired position the pilot has to drive his plane ${53^\circ }$ west to the north in presence of wind, which is blowing in due east. The time is taken by the pilot to reach his destination in $10\;hr$. The velocity of wind is
(A) $\dfrac{{100}}{3}km/hr$
(B) $\dfrac{{200}}{3}km/hr$
(C) $200km/hr$
(D) $150km/hr$
Answer
219.9k+ views
Hint: Here it is given in the question that the pilot wants to go towards the north direction but due to the air flowing it gets drift by some angle. Hence the velocity of the air coming from the east can be evaluated by using the components of the velocity in a particular direction.
Formula used:
Velocity component formula
$V\cos \theta = \dfrac{d}{t}$
where $d$ is the distance and $t$ is time.
Complete step-by-step solution:
We will first consider the component of the velocity of the plane ${V_p}$ at a given particular angle $53^\circ $ which can be seen in the figure given.
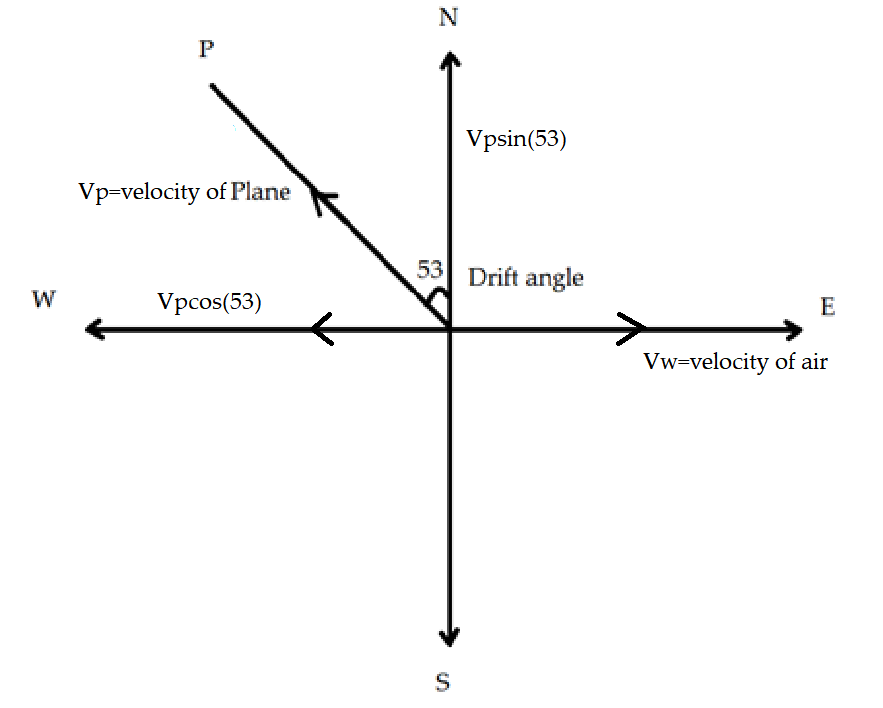
Here from the figure, it can be seen that the velocity components of the plane in the direction of the west are given as ${V_p}\cos {53^\circ }$and in the direction of north given as ${V_p}\sin {53^\circ }$.
Hence the velocity of the air ${V_w}$ coming from the east can be given by component of the velocity in a particular direction as ${V_w}\cos \theta $. Therefore the component of velocity of air can be given by the velocity of the plane, therefore
${V_P} = {V_w}\cos \theta $ ……….$(1)$
Now the velocity of the plane can be given by the velocity formula,
${V_p} = \dfrac{d}{t}$
Substitute the value of distance given $d = 500km$ and the time has taken is $t = 10hr$, hence
${V_p} = \dfrac{{500km}}{{10hr}}$
$\therefore {V_p} = 50km/hr$ ………. $(2)$
Now substitute the value of the equation $(2)$ in the equation $(1)$, hence
$50km/hr = {V_w}\cos {37^\circ }$
$ \Rightarrow 50km/hr = {V_w}\cos (90 - {37^\circ })$
We know that $\cos (90 - \theta ) = \sin \theta $
$\therefore 50km/hr = {V_w}\sin ({53^\circ })$
Substitute the value of $\sin {53^\circ } = \dfrac{3}{4}$ in the equation given
${V_w}\sin {53^\circ } = 50km/hr$
$ \Rightarrow {V_w} \times \dfrac{3}{4} = 50km/hr$
Now transposition of the terms on both side to evaluate to a value of the velocity of air ${V_w}$,
${V_w} = \dfrac{4}{3} \times 50km/hr$
$ \Rightarrow {V_w} = \dfrac{{200}}{3}km/hr$
Hence the velocity of the air coming from the east direction due to which the plane gets drift given by ${V_w} = \dfrac{{200}}{3}km/hr$.
Hence, the option (A) is the correct answer.
Note: Here to solve this type of question we have considered the $\cos {37^\circ }$ in terms of $\sin {53^\circ }$ by using the trigonometric relations given by $\cos \left( {90 - \theta } \right) = \sin \theta $. Also, we have taken the value of $\sin {53^\circ } = 0.75 \approx \dfrac{3}{4}$ so that our solution can be easily concluded.
Formula used:
Velocity component formula
$V\cos \theta = \dfrac{d}{t}$
where $d$ is the distance and $t$ is time.
Complete step-by-step solution:
We will first consider the component of the velocity of the plane ${V_p}$ at a given particular angle $53^\circ $ which can be seen in the figure given.

Here from the figure, it can be seen that the velocity components of the plane in the direction of the west are given as ${V_p}\cos {53^\circ }$and in the direction of north given as ${V_p}\sin {53^\circ }$.
Hence the velocity of the air ${V_w}$ coming from the east can be given by component of the velocity in a particular direction as ${V_w}\cos \theta $. Therefore the component of velocity of air can be given by the velocity of the plane, therefore
${V_P} = {V_w}\cos \theta $ ……….$(1)$
Now the velocity of the plane can be given by the velocity formula,
${V_p} = \dfrac{d}{t}$
Substitute the value of distance given $d = 500km$ and the time has taken is $t = 10hr$, hence
${V_p} = \dfrac{{500km}}{{10hr}}$
$\therefore {V_p} = 50km/hr$ ………. $(2)$
Now substitute the value of the equation $(2)$ in the equation $(1)$, hence
$50km/hr = {V_w}\cos {37^\circ }$
$ \Rightarrow 50km/hr = {V_w}\cos (90 - {37^\circ })$
We know that $\cos (90 - \theta ) = \sin \theta $
$\therefore 50km/hr = {V_w}\sin ({53^\circ })$
Substitute the value of $\sin {53^\circ } = \dfrac{3}{4}$ in the equation given
${V_w}\sin {53^\circ } = 50km/hr$
$ \Rightarrow {V_w} \times \dfrac{3}{4} = 50km/hr$
Now transposition of the terms on both side to evaluate to a value of the velocity of air ${V_w}$,
${V_w} = \dfrac{4}{3} \times 50km/hr$
$ \Rightarrow {V_w} = \dfrac{{200}}{3}km/hr$
Hence the velocity of the air coming from the east direction due to which the plane gets drift given by ${V_w} = \dfrac{{200}}{3}km/hr$.
Hence, the option (A) is the correct answer.
Note: Here to solve this type of question we have considered the $\cos {37^\circ }$ in terms of $\sin {53^\circ }$ by using the trigonometric relations given by $\cos \left( {90 - \theta } \right) = \sin \theta $. Also, we have taken the value of $\sin {53^\circ } = 0.75 \approx \dfrac{3}{4}$ so that our solution can be easily concluded.
Recently Updated Pages
Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

States of Matter Chapter For JEE Main Chemistry

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26




