Question

A person walks at a velocity $V$ in a straight line forming at an angle $\theta $ with the plane of a plane mirror. What is the relative velocity ${V_{{\text{rel}}}}$ with which he approaches the image?

A. $2V\sin \theta $
B. $2V$
C. $2V\cos \theta $
D. $\dfrac{V}{2}\sin \theta $

Answer 1

Hint: When the object moves towards a plane mirror, the velocity of the image is negative of that of the body, that is, $\mathop {{v_i}}\limits^ \to = - \mathop {{v_o}}\limits^ \to $ . When the object is moving parallel to the plane mirror, the velocity of the image is the same as that of the object, that is, $\mathop {{v_i}}\limits^ \to = \mathop {{v_o}}\limits^ \to $ .


Complete answer:
The vertical and horizontal components of the velocity of the person are as shown in the figure below:

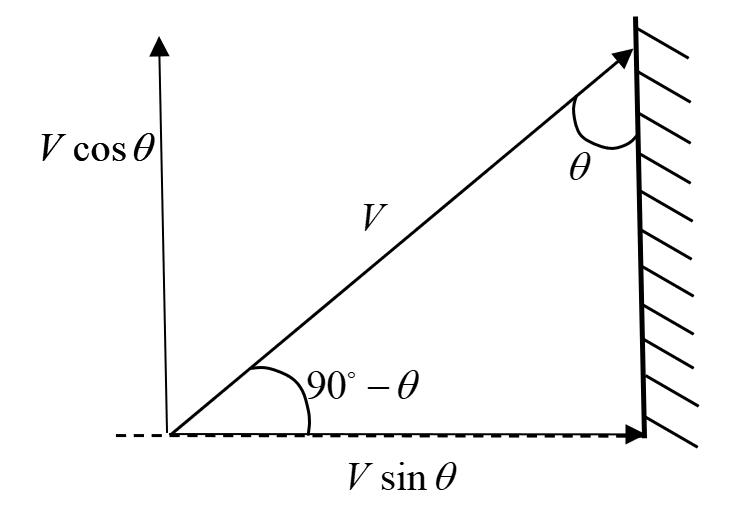
Thus, the velocity of the person is given by:
$\mathop {{V_P}}\limits^ \to = - V\sin \theta \hat i + V\cos \theta \hat j$ … (1)

Now, we know that when the object moves towards a plane mirror, the velocity of the image is negative of that of the body, that is, $\mathop {{v_i}}\limits^ \to = - \mathop {{v_o}}\limits^ \to $ and when the object is moving parallel to the plane mirror, the velocity of the image is the same as that of the object, that is, $\mathop {{v_i}}\limits^ \to = \mathop {{v_o}}\limits^ \to $ .

Apply this concept on the vertical and horizontal components of the image velocity as well.

Let us first consider the vertical components,
In this case, the object is moving parallel to the mirror, therefore, $\mathop {{v_i}}\limits^ \to = \mathop {{v_o}}\limits^ \to $ .
Hence, vertical component of image velocity = vertical component of the velocity of the person
Thus, vertical component of image velocity $ = V\cos \theta $ … (2)

Now, let’s consider the horizontal components,
In this case, the object is moving towards the mirror, therefore, $\mathop {{v_i}}\limits^ \to = - \mathop {{v_o}}\limits^ \to $ .
Hence, horizontal component of image velocity = negative of the horizontal component of the velocity of the person
Thus, horizontal component of image velocity $ = V\sin \theta $ … (3)
Combining (2) and (3),
The velocity of the image, $\mathop {{V_I}}\limits^ \to = V\sin \theta \hat i + V\cos \theta \hat j$ … (4)

Now, velocity of the person with respect to their image, $\mathop {{V_{PI}}}\limits^ \to = \mathop {{V_P}}\limits^ \to - \mathop {{V_I} = }\limits^ \to - 2V\sin \theta \hat i$ .
The magnitude of this velocity is $2V\sin \theta $ .
Thus, the correct option is A.


Note: In the above question, we broke the components of the velocity of the object first. Then, we approached calculating the velocity of the image for each component in order to get our final answer.