Question

A person aiming to reach the exact opposite point on the bank of a stream is swimming with a speed of 0.5 m/s at an angle of 120° with the direction of the flow of water. The speed of water in the stream is:
A) 1 m/s
B) 0.5 m/s
C) 0.25 m/s
D) 0.433 m/s

Answer 1

Hint: if the person starts moving perpendicular to the flow of the stream he cannot reach the exact opposite point on the bank of the stream. Because there are two vectors, one the direction of the flow of the stream and the second the direction of the person which is directly perpendicular to the flow of the stream. Their resultant vector will lead the person to a different point on the bank of the stream. Therefore, man is swimming at an angle of 120 degrees with the direction of the flow. The cosine component of the person’s direction should be equal to the velocity of the stream. Thus, we can calculate the velocity of the stream.

Complete step by step solution:
Step1: Consider the following figure.
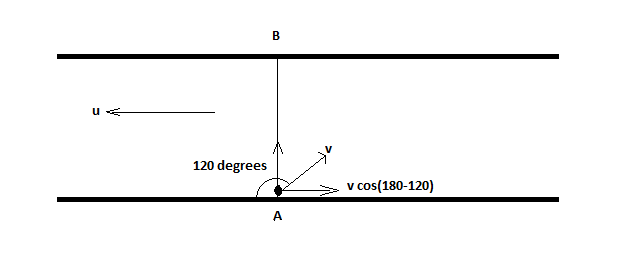In the above diagram, the cosine component of the vector v should be equal to the velocity of the stream. Then only the person can reach the exact opposite point on the bank of a stream. The resultant vector of $\overrightarrow v $ and $\overrightarrow u $ is directly perpendicular to the flow of the stream and thus the person can reach the desired position. Therefore,
$\therefore v\cos (180^\circ - 120^\circ) = u$
Step 2: substitute the value 0.5 m/s for $v$
$\therefore 0.5 \times \cos 60^\circ = u$
$ \Rightarrow u = 0.5 \times 0.5$
$ \Rightarrow u = 0.25m/s.$
Therefore, the speed of the stream is 0.25 m/s.

Thus, the correct answer is Option C.

Note: This is the concept of vector addition. If we assume that at a point two forces are acting and there is an angle $\theta $ between them. Then the resultant vector of the force vectors is the direction where the point moves. In the above question also two forces are acting on the person, first by the flow of the stream in the direction of flow second by the person himself to move in water in the direction of the 120 degrees with the stream. The resultant vector in this case is perpendicular to the flow of the stream.