Question

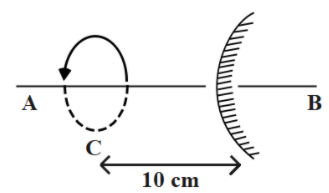
A particle revolves in clockwise direction (as seen from point A) in a circle C of radius 1 cm and completes one revolution in 2 sec. The axis of the circle and the principal axis of the mirror M coincide, call it AB. The radius of curvature of the mirror is 20 cm. Then, the direction of revolution (as seen from A) of the image of the particle and its speed is



A. Clockwise, $1.57c{m^{ - 1}}$
B. Clockwise, $3.14c{m^{ - 1}}$
C. Anticlockwise, $1.57c{m^{ - 1}}$
D. Anticlockwise, $3.14c{m^{ - 1}}$

Answer 1

Hint: Given are the object distance and focal length of the convex mirror, using mirror formula to find the image distance. Then substitute its value to the mathematical expression for magnification of the image produced. Later use the relation of the time period and angular velocity to find the required speed.

Formula Used:
Mirror Formula:
$\eqalign{
  & \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \cr
  & {\text{where }}v{\text{ is the distance of image from optical center,}} \cr
  & u{\text{ is the distance of object from optical center,}} \cr
  & f{\text{ is the focal length of the mirror used}}{\text{.}} \cr} $
Magnification produced by mirror is, $m = \dfrac{{ - v}}{u}$
Time Period, $T = \dfrac{{2\pi }}{\omega }$
Relation between linear velocity and angular velocity: $v = r \times \omega $

Complete step by step answer:
The rotating particle will result in a virtual image being formed by the convex mirror.
Given:
The distance of object from optical center, $u = - 10cm$
The radius of curvature of the convex mirror, $C = 20cm$
The focal length of the convex mirror, $f = \dfrac{C}{2} = \dfrac{{20}}{2} = 10cm$
Time Period of one revolution, $T = 2\sec $
Applying mirror formula to the given values we get:
$\eqalign{
  & \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \cr
  & \Rightarrow \dfrac{1}{v} + \dfrac{{ - 1}}{{10}} = \dfrac{1}{{10}} \cr
  & \Rightarrow \dfrac{1}{v} = \dfrac{1}{{10}} + \dfrac{1}{{10}} = \dfrac{2}{{10}} \cr
  & \Rightarrow v = \dfrac{{10}}{2} \cr
  & \therefore v = + 5cm \cr} $
So, the magnification of the image produced by the mirror is:
$\eqalign{
  & m = \dfrac{{ - v}}{u} \cr
  & \Rightarrow m = \dfrac{{ - 5}}{{ - 10}} \cr
  & \therefore m = 0.5cm \cr} $
We known that time period of one revolution is mathematically equal to the ratio of twice pi upon the angular velocity, so we have:
$\eqalign{
  & T = \dfrac{{2\pi }}{\omega } \cr
  & \Rightarrow 2 = \dfrac{{2\pi }}{\omega }{\text{ }}\left[ {\because T = 2\left( {{\text{given}}} \right)} \right] \cr
  & \therefore \omega = \pi \cr} $
Now, the linear velocity is related to the angular velocity by the following relation:
$\eqalign{
  & v = r \times \omega \cr
  & {\text{where }}r{\text{ is the magnification in this case}} \cr} $
Substituting values in the above equation we get:
$\eqalign{
  & v = r \times \omega \cr
  & \Rightarrow v = 0.5 \times \pi \cr
  & \Rightarrow v = 0.5 \times 3.14 \cr
  & \therefore v = 1.57c{m^{ - 1}} \cr} $
And the direction of revolution will be the same as the object that is in clockwise direction.
Therefore, the correct option is A i.e., Clockwise, $1.57c{m^{ - 1}}$

Note: Similar to plane mirrors, convex mirrors also produce virtual images. Additionally, the image formed is upright and reduced in size than the original object. It is located behind the mirror. Whereas in the concave mirror the characteristics of the formed image gets altered based on the location of the object on the optical axis.