
A particle of mass $M$ and charge $Q$ moving with velocity $\vec{v}$ describes a circular path of the radius $R$ when subjected to a uniform transverse magnetic field of induction $B$. The work done by the field when the particle completes one full circle is
A.$BQv2\pi R$
B.$\left( \dfrac{M{{v}^{2}}}{R} \right)2\pi R$
C. Zero
D.$BQ2\pi R$
Answer
217.8k+ views
Hint: When a particle of mass $M$ and charge $Q$ moving with velocity $\vec{v}$ describes a circular path in a magnetic field, the magnetic force acting on the particle will be perpendicular to the magnetic field and its velocity. Therefore the kinetic energy of the particle remains constant.
Formula used:
Power is given by the scalar dot product of force and velocity vector.
$P=\vec{F}.\vec{v}$
$P=$power
$F=$magnetic force
$v=$velocity of particle
And work done,$w=P\times t$
$t=$time
Complete answer:
A particle experiences a magnetic force when moving through a magnetic field. When a charged particle of mass $M$ moves with velocity$\vec{v}$, perpendicular to the uniform magnetic field $B$, this particle follows the curved path until it forms a complete circular path.
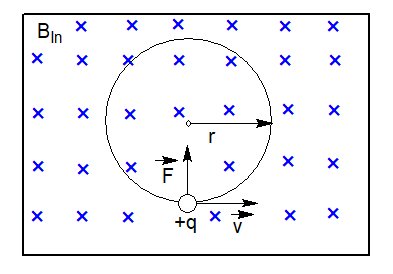
Fig. $q$ charged particle completes a full circle.
Or, in other words, the magnetic force is always perpendicular to the velocity,$\vec{v}$so that the net power transferred by it to the particle will be zero.
$P=\vec{F}.\vec{v}$
Or, $P=Fv\cos \theta $
Or, $P=Fv\cos {{90}^{o}}$ [Since $\theta =$ the angle between the magnetic force and velocity]
Or, $P=0$
Again power $p$is defined as the rate at which work is done.
$P=\dfrac{work}{time}=\dfrac{W}{t}$
Or,$W=P\times t$
As we know from above the net power on the particle is zero, thus putting this value we get,
$W=0\times t=0$
Whenever the magnetic force is perpendicular to the velocity, it does not work on the charged particle. Then the kinetic energy and velocity remain constant. This is because the direction of motion is affected but not the magnitude of velocity.
Hence, the work done by the field when the particle completes one full circle is zero.
Thus, option (C) is correct.
Note:If an electron is in the region where the electric field, magnetic field, and direction of velocity are parallel to each other, then the force due to the magnetic field is zero. The charged particle will be accelerated by the electric field only.
Formula used:
Power is given by the scalar dot product of force and velocity vector.
$P=\vec{F}.\vec{v}$
$P=$power
$F=$magnetic force
$v=$velocity of particle
And work done,$w=P\times t$
$t=$time
Complete answer:
A particle experiences a magnetic force when moving through a magnetic field. When a charged particle of mass $M$ moves with velocity$\vec{v}$, perpendicular to the uniform magnetic field $B$, this particle follows the curved path until it forms a complete circular path.

Fig. $q$ charged particle completes a full circle.
Or, in other words, the magnetic force is always perpendicular to the velocity,$\vec{v}$so that the net power transferred by it to the particle will be zero.
$P=\vec{F}.\vec{v}$
Or, $P=Fv\cos \theta $
Or, $P=Fv\cos {{90}^{o}}$ [Since $\theta =$ the angle between the magnetic force and velocity]
Or, $P=0$
Again power $p$is defined as the rate at which work is done.
$P=\dfrac{work}{time}=\dfrac{W}{t}$
Or,$W=P\times t$
As we know from above the net power on the particle is zero, thus putting this value we get,
$W=0\times t=0$
Whenever the magnetic force is perpendicular to the velocity, it does not work on the charged particle. Then the kinetic energy and velocity remain constant. This is because the direction of motion is affected but not the magnitude of velocity.
Hence, the work done by the field when the particle completes one full circle is zero.
Thus, option (C) is correct.
Note:If an electron is in the region where the electric field, magnetic field, and direction of velocity are parallel to each other, then the force due to the magnetic field is zero. The charged particle will be accelerated by the electric field only.
Recently Updated Pages
Arithmetic, Geometric & Harmonic Progressions Explained

Cartesian Form of Vector Explained: Formula, Examples & Uses

Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Trending doubts
Understanding Collisions: Types and Examples for Students

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding the Wheatstone Bridge: Principles, Formula, and Applications

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

JEE Main 2025-26 Mock Test: Ultimate Practice Guide for Aspirants

Other Pages
MOSFET: Definition, Working Principle, Types & Applications

Diffraction of Light - Young’s Single Slit Experiment

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

JEE Main 2025-26 Chapter-Wise Mock Test Preparation Guide

Understanding Elastic Collisions in Two Dimensions




