Question

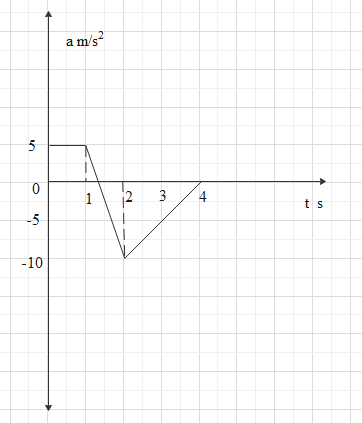
A particle moves along x-axis with initial velocity $5\,m/s$. If acceleration a varies with time t as shown in a-t graph, then the velocity of the particle just after 4 second is

A. $ - 2.5\,m/s$
B. $10\,m/s$
C. $ - 1.25\,m/s$
D. $5\,m/s$

Answer 1

Hint: We know that the area under the acceleration time graph gives us the change in velocity(final velocity - initial velocity) under proper limits. If you find the area under the graph from zero to four seconds and add the value to the initial velocity, we will get the final velocity at 4 seconds.

Complete step by step answer:
It is given that a particle is moving along the x axis.
The initial velocity of the particle is given as
${v_o} = 5\,m/s$
We need to find the velocity of the particle at time
$t = 4\,s$
We know that the area under the acceleration time graph gives us the velocity.
So, if you find the total area under the curve from 0 to 4 seconds then we can find the final velocity.
Now let us calculate the area.
We can calculate the area of each section separately.

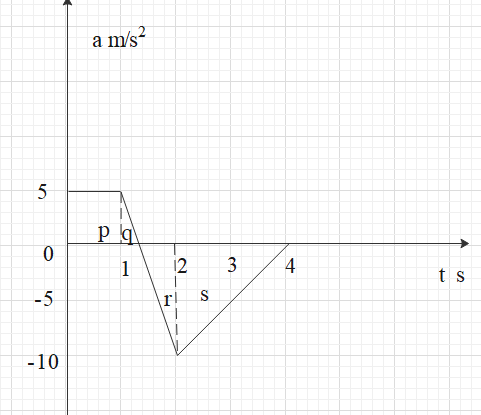
Area p represents the area of a square.
We know that area is calculated as a product of length and breadth.
From the graph we can see that the length is $l = 5$
Breadth is $b = 1$
This area is $p = l \times b = 5$
Now the area q represents the area of a right-angled triangle.
Area of a right-angled triangle is half the base multiplied by the height.
Here we need to calculate the length of the base. Let the base be $x$. Then the base of the next triangle with area r will be $1 - x$ .
We can see that both these triangles q and r are similar because two angles are equal.
Hence, the ratio of corresponding sides will be the same.
$ \Rightarrow \dfrac{5}{x} = \dfrac{{10}}{{1 - x}}$
$ \Rightarrow 1 - x = 2x$
$ \Rightarrow x = \dfrac{1}{3}$
Now area of the triangle q is
$q = \dfrac{1}{2} \times 5 \times \dfrac{1}{3}$
Since base is x and height is 5.
$ \Rightarrow q = \dfrac{5}{6}$
Area of the second triangle is
$r = \dfrac{1}{2} \times 10 \times \dfrac{2}{3}$
Since, the base of this triangle is $1 - x = 1 - \dfrac{1}{3} = \dfrac{2}{3}$ and height is 10.
$ \Rightarrow r = \dfrac{{10}}{3}$
Area of the third triangle s is
$s = \dfrac{1}{2} \times 2 \times 10$
$ \Rightarrow s = 10$
If we add all these areas, we will get the change in velocity.
Here the areas r and s lie below the x axis. Since it is in the negative y direction, we need to take negative signs.
$ \Rightarrow \Delta v = p + q - r - s$
$ \Rightarrow \Delta v = 5 + \dfrac{5}{6} - \dfrac{{10}}{3} - 10$
$ \Rightarrow \Delta v = - 7.5$
The particle starts with an initial velocity ${v_o} = 5\,m/s$
So, at 4 seconds, the final velocity is
$ \Rightarrow v = {v_0} + \Delta v$
On substituting the values, we get.
$ \Rightarrow v = 5 - 7.5$
$ \Rightarrow v = - 2.5\,m/s$
This is the value of velocity just after 4 seconds.
Hence the correct answer is option A.

Note: Remember that while calculating the area we should take care of the quadrant in which the area lies. In the given graph the area from 2 seconds to 4 seconds lies in the negative y direction. So, we should subtract this area from the area about the x axis.